Problem G: Yu-kun Likes People Watching
Background
会津大学付属幼稚園はプログラミングが大好きな子供が集まる幼稚園である。園児の一人であるゆう君は、プログラミングと同じくらい人を観察することが大好きだ。 そんなゆう君は、去年の夏休みに作成した人の移動経路のデータと建物の位置情報を観察してあることを疑問に思った。 全ての人が建物内にいる時間の長さのうち、最長のものはどのくらいなのだろうか?
Problem
建物と人の移動経路の情報が与えられる。 全ての人が連続して建物内にいるような時間のうち、最も長いものの長さを出力せよ。 そのような時間が存在しない場合は長さは0とする。 建物と人はそれぞれ2次元平面上の多角形と点として表される。 人は単位時間あたりx軸方向とy軸方向にそれぞれ速度vxとvyで移動する。 人を表す点が建物を表す多角形内にある場合、その人は建物内にいるものとする。 ( 多角形の辺上に人がいる場合も建物内にいるものとする )
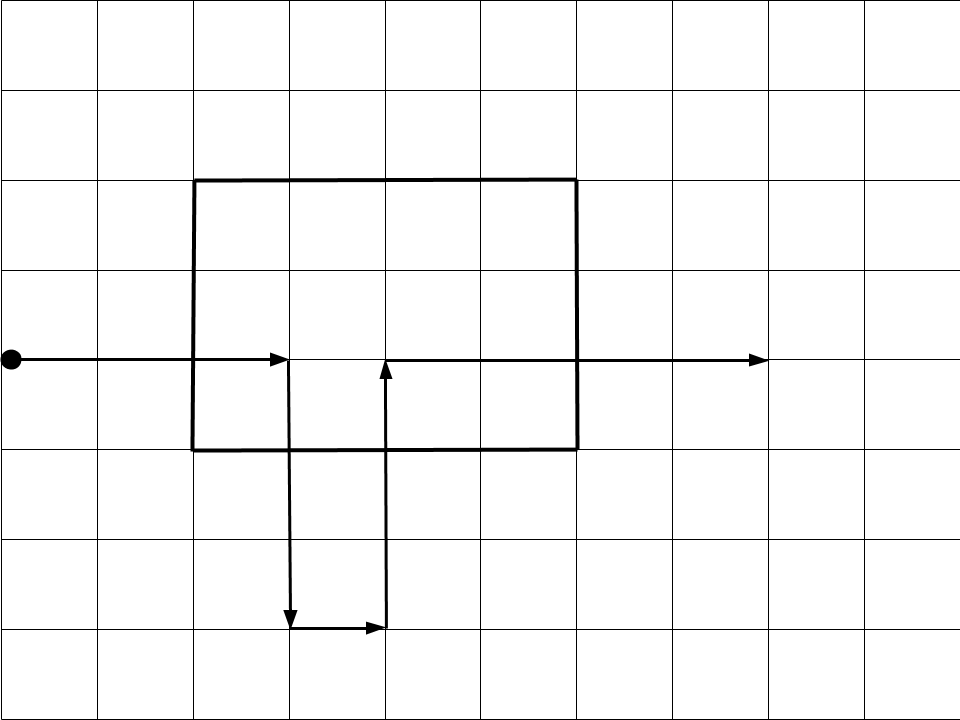
図1は、Sample Input 2 における建物と人の移動経路を表している。多角形は建物、黒い丸は人の初期位置、矢印はその人の移動経路を表す。 時刻2から時刻4、時刻9から時刻12の間に人は建物内にいるため、建物内に全ての人がいる時間の最長は3となる。
| 図1: Sample Input 2 |
Input
n m T 建物0の情報 建物1の情報 ... 建物n-1の情報 人0の移動経路 人1の移動経路 ... 人m-1の移動経路
n,m,Tはそれぞれ建物を表す多角形の数、人の数、人が移動する時間の上限を表す。
建物の情報は以下のような形式で与えられる。 (xi,yi)と(xi+1,yi+1)の頂点を繋いだ線分が多角形の一辺である。ただし、p-1番目の頂点とは、0番目の頂点が繋がる。
p x0 y0 x1 y1 ... xp-1 yp-1
人の経路情報は以下のような形式で与えられる。
t0 sx0 sy0 ( t0 = 0 ) t1 vx1 vy1 t2 vx2 vy2 ... tk vxk vyk ( tk = T )
人は2次元平面上を移動する。 (sx0,sy0) は人が時刻0にいる位置である。 時刻ti-1からtiの間( 0 < i ≤ k ), x軸方向とy軸方向にそれぞれ速度vxiとvyiで移動する。
Constraints
入力は以下の条件を満たす。
- 入力は全て整数として与えられる
- 1 ≤ n, m ≤ 10
- 3 ≤ p ≤ 10
- 1 ≤ T ≤ 3600
- 0 ≤ x, y, sx, sy ≤ 1000
- 0 = t0 < t1 < ... < tk = T
- -10 ≤ vx1,vy1,...,vxk,vyk ≤ 10
- 建物を表す多角形は時計回りまたは反時計周りで与えられる
- 多角形の連続する3つの頂点は、一直線上に並ばないものとする
- 人の位置は常に0以上1000以下である
- 同じ時刻に2人以上の人が同じ座標にいても良い
- 建物が別の建物を内包するようなことはない
- 建物を表す多角形の辺が別の建物を表す多角形の辺と共通な部分をもつことはない
Output
全ての人が建物内にいるような時間のうち、その長さが最長のものの長さを1行で出力せよ。 そのような時間がない場合、長さは0とする。 小数点以下は何桁数字を出力しても構わない。ただし、解答の誤差は0.000001(10-6)を超えてはならない。
Sample Input 1
1 1 10 4 3 0 7 0 7 10 3 10 0 0 5 10 1 0
Sample Output 1
4.0000000000
Sample Input 2
1 1 14 4 2 3 6 3 6 6 2 6 0 0 4 3 1 0 6 0 -1 7 1 0 10 0 1 14 1 0
Sample Output 2
3.0000000000
Sample Input 3
2 2 7 4 2 2 5 2 5 5 2 5 4 7 2 10 2 10 5 7 5 0 0 4 3 1 0 7 0 -1 0 7 7 2 1 0 5 0 -1 7 1 0
Sample Output 3
1.0000000000
Sample Input 4
1 3 10 9 2 3 3 6 4 3 5 6 6 3 7 6 8 3 8 7 2 7 0 1 5 10 1 0 0 11 4 10 -1 0 0 4 8 6 0 -1 8 1 0 10 0 1
Sample Output 4
0.3333333333
Sample Input 5
1 2 7 4 2 1 6 1 6 5 2 5 0 1 4 7 1 0 0 9 3 7 0 1
Sample Output 5
0.0000000000