複雑な折り紙

折り紙の権威で，国際紙細工文化協会（Intercultural Consortium on Paper Crafts）の理事でもある G 博士は，折り紙は作られる図形が複雑なほど美しいという信念を持っている．あなたは博士の助手として，最も複雑な形が得られる折り方を見つけなければならない．博士が言うには，図形の複雑さとは，頂点の個数が多いことであり，頂点数が同じ場合には周長が長いことである．ただし，問題を簡単にするため，凸多角形を一度だけ折る場合について考え，紙を折るときには必ずある頂点が別の頂点に重なるように折らなければならないものとする．

凸多角形が与えられたとき，一度だけ折り返してできる多角形の中で，最も複雑なものの周長を出力するプログラムを書け．

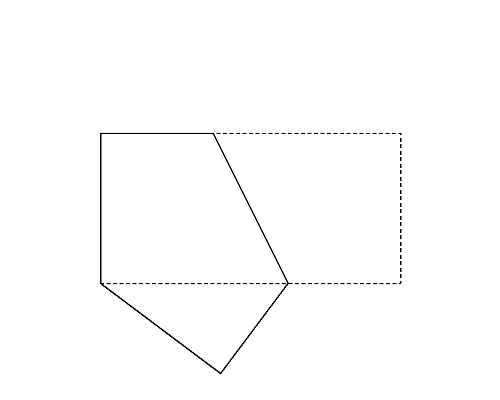
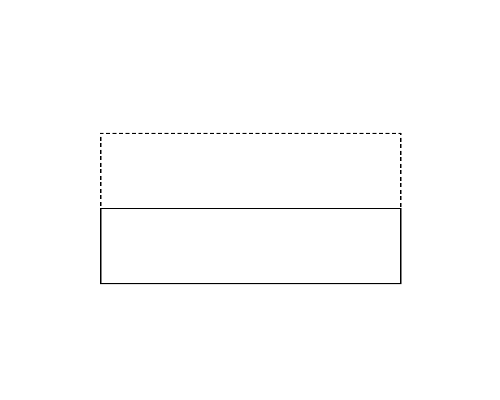
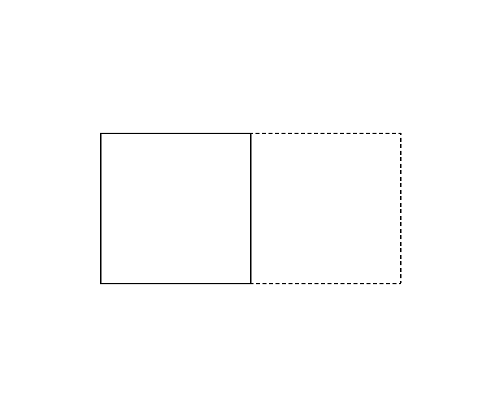
図1左は，Sample Input の最初のデータセットに記述された多角形で，長方形である．これを折ると図1-a〜c の実線で示すように 3 通りの多角形を作ることができる．このデータセットに対しては，この中で最も頂点数の多い五角形（図1-a）の周長を答えればよい．図1-a よりも図1-b の長方形の方が周長は長いが，頂点数の多い方が優先される．


	(a)	(b)	(c)

図1: 第1サンプルインプットの場合

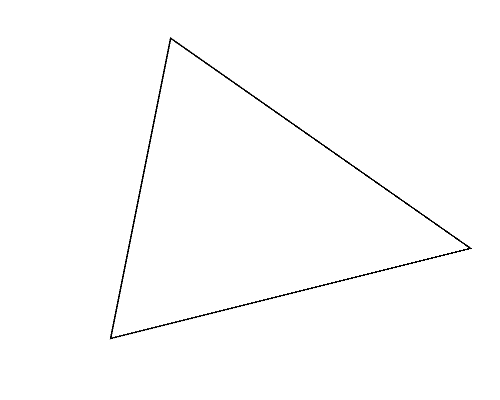
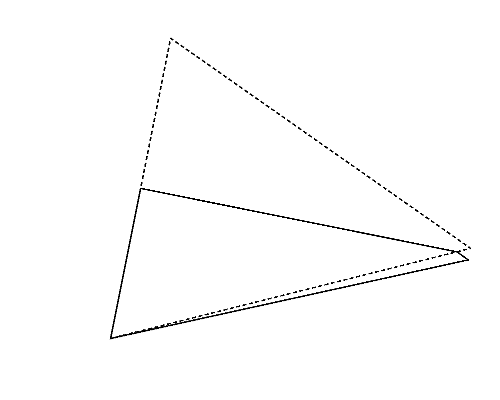
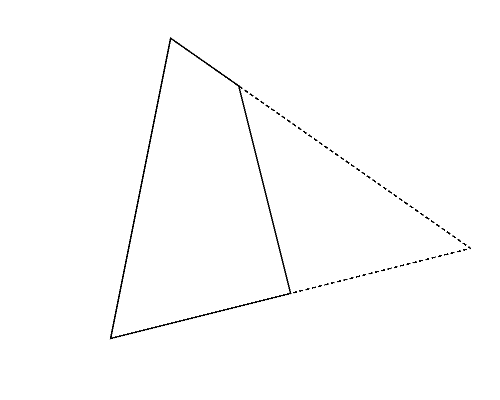
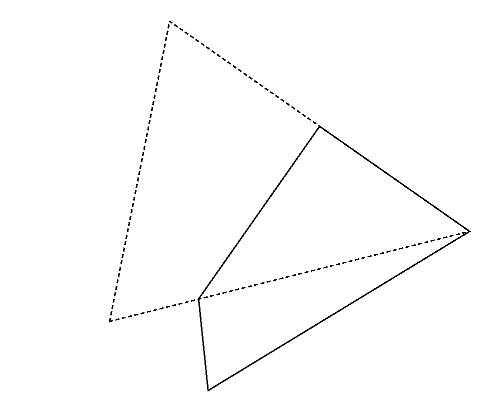
図2左は，Sample Input の 2 番目のデータセットに記述された多角形で，三角形である．この三角形は，どのように 2 頂点を選んでも，それらを重ねるように折ると四角形（図2-a〜c）になる．これらの中から，最も長い周長（この場合は図2-a の周長）を答えればよい．


	(a)	(b)	(c)

図2: 第2サンプルインプットの場合

入力として与えられる多角形は凸に限られるが，これを折って得られる多角形は凹であるかもしれない．図3左は，Sample Input の 3 番目のデータセットに記述された多角形である．この多角形は，折ると凹六角形になる場合（図3右）があり，このとき最も頂点数が多くなる．

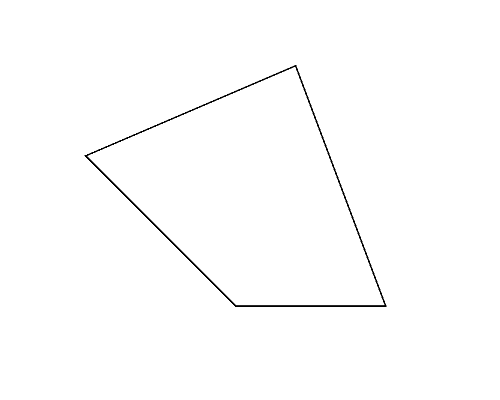
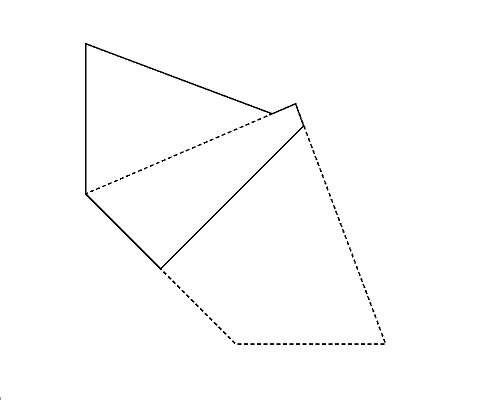
図3: 第3サンプルインプットの場合

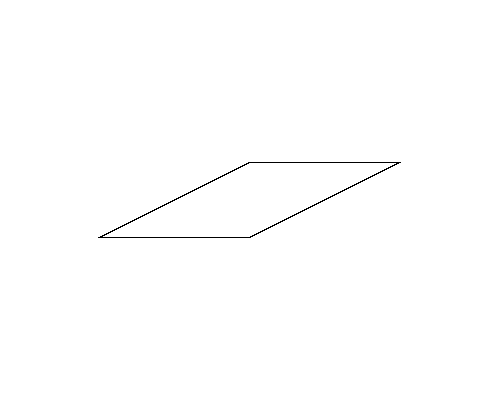
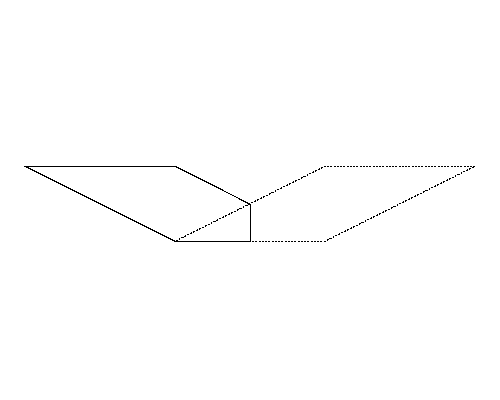
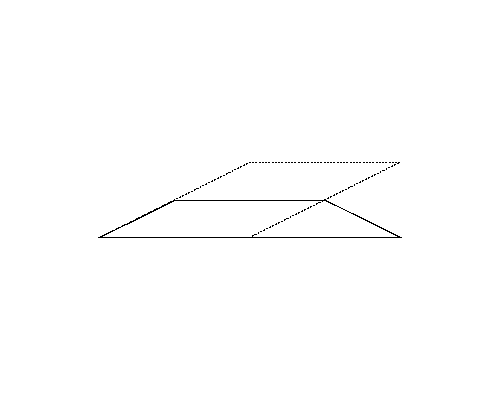
図4左は，Sample Input の 5 番目のデータセットに記述された多角形である．図4-bの図形は図4-aの図形よりも周長が長いが，図4-bの図形は四角形であるので，正解は図4-aの五角形の周長となる．


	(a)	(b)

図4: 第5サンプルインプットの場合

Input

入力は複数のデータセットからなる．各データセットは次の形式で表される．

n
x₁ y₁
...
x_n y_n

ここで n は最初に与えられる多角形の頂点数であり， 3 ≤ n ≤ 20 を満たす正整数である． x_iとy_iは 0 ≤ x_i,y_i < 1000 を満たす整数で， (x_i, y_i) は i 番目の頂点の座標を与える．また，頂点の列 (x₁, y₁), ..., (x_n, y_n) は y 軸を上向きとする xy 平面上で反時計回りに順番に並んでおり，こうして与えられる多角形が凸であることは保証されている．

ここで入力に与えられる多角形の任意の 2 頂点を重ねるように折って得られる多角形について，以下のふたつの条件が成り立つものと仮定してよい．

多角形の頂点間の距離は，いずれも 0.00001 以上である．
多角形の連続する 3 頂点 P, Q, R について，点 Q と点 P, R を通る直線との距離は 0.00001 以上である．

入力の終わりは，ゼロだけからなる行で表される．

Output

各データセットについて，与えられた多角形を折ることで得られる多角形で最も複雑なものの周長を出力せよ．出力には 0.00001 以上の誤差を含んではならない．それ以外の余計な文字を出力してはならない．

Sample Input

Output for the Sample Input

23.090170
28.528295
23.553450
97.135255
34.270510
57.124116
3327.900180
142.111776

Source: https://onlinejudge.u-aizu.ac.jp/problems/1606