文字解読
謎の組織が残した画像データが発見された.あなたは,この画像データを解析することを依頼された.その組織では独自の文字が用いられていて,それぞれの文字は白い紙に黒インクで記したものが,2 値画像として表されている.
それぞれの文字を表現する画像には多くのバリエーションが存在するが,ふたつの画像が同じ文字を表すかどうかは連結成分の包含関係で判定できることがわかった.ここでは以下の用語を定義する.なお,画像の範囲外は白のピクセルで埋まっているものと考える.
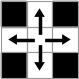
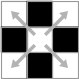
- 白の連結成分 : 縦横につながっている白ピクセルからなる集合. (下図)
- 黒の連結成分 : 縦横斜めにつながっている黒ピクセルからなる集合. (下図)
- 連結成分 : 白または黒の連結成分.
- 背景連結成分 : 画像範囲外のピクセルを含む連結成分.画像の最外側の白ピクセルは背景連結成分の一部になる.
 |
 |
 |
 |
| 連結 | 非連結 | 連結 | 連結 |
| 白の連結性 | 黒の連結性 | ||
C1 をある画像のひとつの連結成分,C2 を同じ画像の反対色の連結成分とする.ここで C1, C2 以外のピクセルを,すべて C2 の色に変えた画像を考える.C1 と C2 が共に背景連結成分でないならば,背景連結成分の色もC2 の色に変える.そのように変更した画像でも C2 のピクセルが背景連結成分に含まれないとき,元の画像について C1 は C2 を包含するという.(下図)
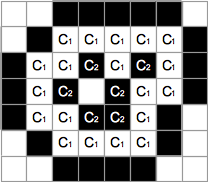
ふたつの画像は以下の両条件が満たされるとき同じ文字を表す.
- 両画像は同数の連結成分を持つ.
- ふたつの画像に含まれる連結成分の集合をそれぞれ S, S' とすると,以下の両条件を満たす全単射 f : S → S' が存在する.
- S のすべての要素 C について,C の色と f (C) の色は同じである.
- S のすべての要素 C1, C2 について,C1 が C2 を包含することが f (C1) が f (C2) を包含することの必要十分条件である.
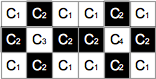
例を示す.下図の画像中の連結成分は以下の包含関係を持つ.
- C1 が C2 を包含する.
- C2 が C3 を包含する.
- C2 が C4 を包含する.
- C'1 が C'2 を包含する.
- C'2 が C'3 を包含する.
- C'2 が C'4 を包含する.
これらの各連結成分について,f (Ci) = C'iで定義される全単射は上述の条件を満たしている.したがって,左の画像と右の画像は同じ文字を表していることが分かる.
 |
 |
与えられた ふたつの画像が同じ文字を表すかどうかを判定するプログラムを作成しなさい.
Input
入力は最大で 200 個のデータセットからなる.入力の終わりはゼロふたつからなる行である.各データセットは次の形式をしている.
画像 1
画像 2
各画像は以下の形式をしている.
h w
p(1,1) ... p(1,w)
...
p(h,1) ... p(h,w)
h と w は画像の高さと幅のピクセル数であり,1 ≤ h ≤ 100, 1 ≤ w ≤ 100 と仮定して良い.続く h 行はそれぞれ w 個の文字からなる.p(y,x) は,左上隅から数えて上から y 番目,左から x 番目のピクセルの色を表す文字である.文字は白を表すピリオド (".") と黒を表すシャープ ("#") のいずれかである.
Output
入力データセットごとに,ふたつの画像が同じ文字を表すときには "yes", さもなければ "no" をそれぞれ 1 行に出力しなさい.出力には余分な文字を含んではならない.
Sample Input
3 6 .#..#. #.##.# .#..#. 8 7 .#####. #.....# #..#..# #.#.#.# #..#..# #..#..# .#####. ...#... 3 3 #.. ... #.. 3 3 #.. .#. #.. 3 3 ... ... ... 3 3 ... .#. ... 3 3 .#. #.# .#. 3 3 .#. ### .#. 7 7 .#####. #.....# #..#..# #.#.#.# #..#..# #.....# .#####. 7 7 .#####. #.....# #..#..# #.#.#.# #..#..# #..#..# .#####. 7 7 .#####. #.....# #..#..# #.#.#.# #..#..# #.....# .#####. 7 11 .#####..... #.....#.... #..#..#..#. #.#.#.#.#.# #..#..#..#. #.....#.... .#####..... 7 3 .#. #.# .#. #.# .#. #.# .#. 7 7 .#####. #..#..# #..#..# #.#.#.# #..#..# #..#..# .#####. 3 1 # # . 1 2 #. 0 0
Output for the Sample Input
yes no no no no no yes yes