折り紙

マスター・グルスは有名な折り紙芸術家であり，折り紙芸術の可能性の探求に熱中している． 将来の創作のために，今は，折り紙の一般理論を目指した基礎的実験を計画しているところである．

実験には長方形の紙を使う． 紙を水平または垂直に何回か折り，その後，折り畳んだ紙を貫通する穴をいくつかあける．

次の図は簡単な実験での紙を折る過程を示している． これは Sample Input の 3 番目のデータセットに対応している． 左上に示す 10 × 8 の長方形の紙を 3 回折ると，右下の 6 × 6 の正方形の形になる． この図では，破線が折り線を表し，弧状の矢印が折る方向を表す． 長方形の大きさと正確な折る場所を示すために，実線が縦横に等間隔で引かれている． そして，長方形領域の色の濃さで，重なった紙の枚数を表している． 折り畳んだ紙の A, B の箇所に穴を貫通させると，紙には全部で 9 つの穴 (A で 8 つ，B で 1 つ) があく．

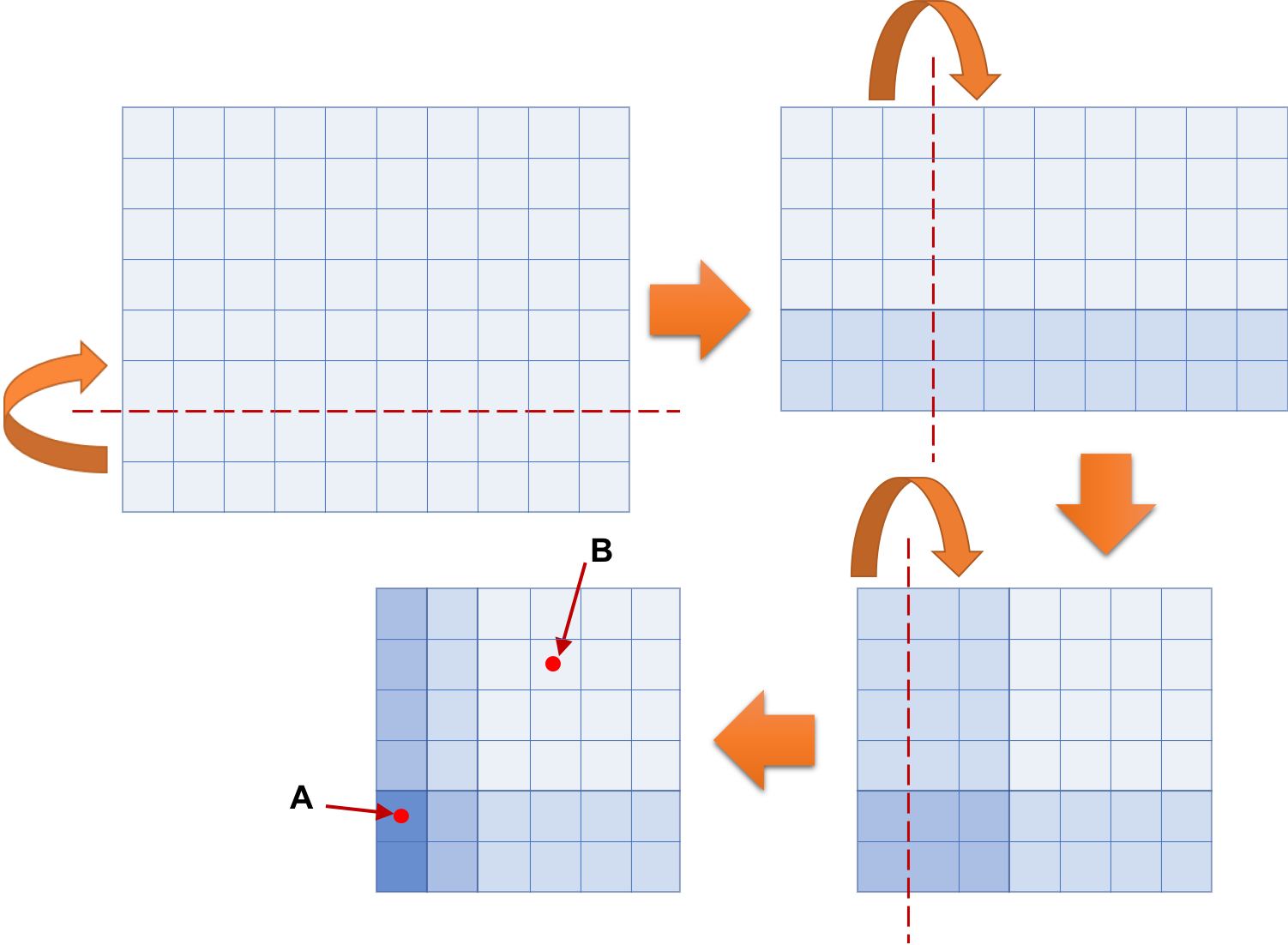
この問題でのあなたの仕事は，長方形の紙と折ったり穴をあけたりする操作に関する情報から，紙に何個の穴があくかを求めるプログラムを作ることである．

Input

入力は高々 1000 個のデータセットからなる． 各データセットは次の形式で表される．

n m t p
d₁ c₁
...
d_t c_t
x₁ y₁
...
x_p y_p

n, m はそれぞれ長方形の紙の幅と高さであり，32 以下の正整数である． t, p はそれぞれ折る操作と穴をあける操作の回数であり，20 以下の正整数である． d_i, c_i の対で i 番目の折る操作を以下のように定める．

• d_i は 1 または 2 である．
• c_i は正整数である．
• もし d_i が 1 なら，左端から c_i だけ右側を通る垂直の折り線の左側を右側に折り重ねる．
• もし d_i が 2 なら，下端から c_i だけ上側を通る水平の折り線の下側を上側に折り重ねる．

最初の i−1 回の折る操作を実行した後，d_i が 1 なら紙の幅は c_i を超え，d_i が 2 なら紙の高さは c_i を超える． (x_i + 1/2, y_i + 1/2) により，i 番目の穴をあける場所が与えられる． 原点 (0, 0) は，紙の最終的な形での左下の点である． x_i と y_i はどちらも非負整数であり，それぞれ，最終的な形の幅と高さより小さい． 穴をあける 2 つ以上の操作が同じ場所に適用されることはないと仮定してよい．

入力の終わりは，4 つのゼロからなる行で表される．

Output

各データセットに対し，p 行の出力を行え． i 行目には i 番目の穴をあける操作で紙にあけられた穴の数を出力すること．

Sample Input

2 1 1 1
1 1
0 0
1 3 2 1
2 1
2 1
0 0
10 8 3 2
2 2
1 3
1 1
0 1
3 4
3 3 3 2
1 2
2 1
1 1
0 1
0 0
0 0 0 0

Output for the Sample Input

2
3
8
1
3
6

---