正三角形の柵

三角氏はまっすぐな道に沿った果樹園を所有している． 最近，果樹園の梨を狙ってイノシシが出没するようになったので，彼女は多くの梨の木を護る柵を作ろうと考えた．

果樹園には n 本の梨の木が生えており，梨の生えている場所は 2 次元座標 (x₁, y₁),..., (x_n, y_n) で与えられる．簡単のため梨の木の太さは無視する． 三角氏の美学から，柵は正三角形で，一辺は道に平行でなければならない． もちろん反対側の頂点は道から遠い側になくてはならない． 梨の木の位置の座標系は，道が y = 0 となるように設定されており，梨の木は y ≥ 1 にある．

予算の都合から，三角氏は最大 k 本の木は柵の外に残してもよいことにした． この条件で柵の最短長を求めよ．

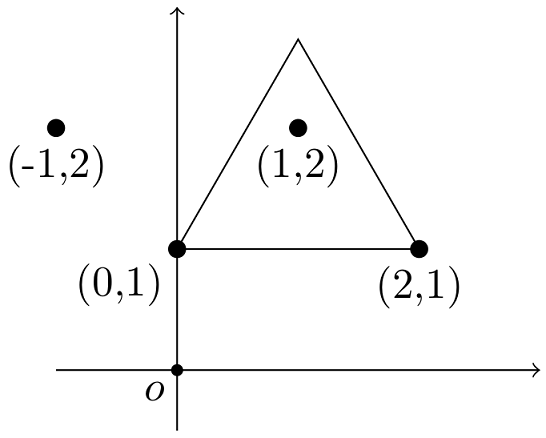
以下の図は Sample Input の最初のデータセットを表している． 4 本の梨の木が座標 (−1,2), (0,1), (1,2), (2,1) にあり，(−1,2) にある梨の木を柵の外に残すことにすると，周長 6 の正三角形が得られる．

Input

入力は複数のデータセットからなる． 各データセットは以下の形式で表される．

n
k
x₁ y₁
...
x_n y_n

各データセットは n+2 行からなる． 1 行目の n は梨の木の本数を表しており，3 ≤ n ≤ 10 000 を満たす． 2 行目の k は柵の外に出てよい梨の木の本数を表しており，1 ≤ k ≤ min(n−2, 5 000) を満たす． 続く n 行は梨の木の座標を表す 2 つの整数 x_i, y_i からなり，−10 000 ≤ x_i ≤ 10 000, 1 ≤ y_i ≤ 10 000 が成り立つ． 相異なる 2 本の梨の木が同じ座標をもつことはない．すなわち (x_i, y_i)=(x_j, y_j) が成り立つのは i=j の場合に限られる．

入力の終わりは，1 個のゼロだけからなる行で表される． データセットの総数は 100 を超えない．

Output

各データセットについて，柵の最短長を表す数を出力せよ．結果は 10⁻⁶ 以上の誤差を含んではいけない．

Sample Input

4
1
0 1
1 2
-1 2
2 1
4
1
1 1
2 2
1 3
1 4
4
1
1 1
2 2
3 1
4 1
4
1
1 2
2 1
3 2
4 2
5
2
0 1
0 2
0 3
0 4
0 5
6
3
0 2
2 2
1 1
0 3
2 3
1 4
0

Output for the Sample Input

6.000000000000
6.928203230276
6.000000000000
7.732050807569
6.928203230276
6.000000000000

---