色の切り替え
無向完全グラフが与えられる. どの頂点どうしもそれぞれ 1 本の赤か黒の辺で結ばれている. 各辺にはペナルティと呼ばれる整数値が設定されている.
このグラフに対してある操作を繰り返すことによって, 赤い辺だけからなる「全域木」を作りたい. すなわち,ちょうど(頂点数 − 1)本の辺だけが赤く, その赤い辺だけで任意の頂点間が直接または間接的につながっているようにしたい. そういう木がいくつも作れるのなら, 赤い辺のペナルティの合計が最小のものを選びたい.
1 回の操作では,頂点をひとつ選び,それに繋がっている全ての辺の色を反転, つまり赤い辺は黒く,黒い辺は赤くする.
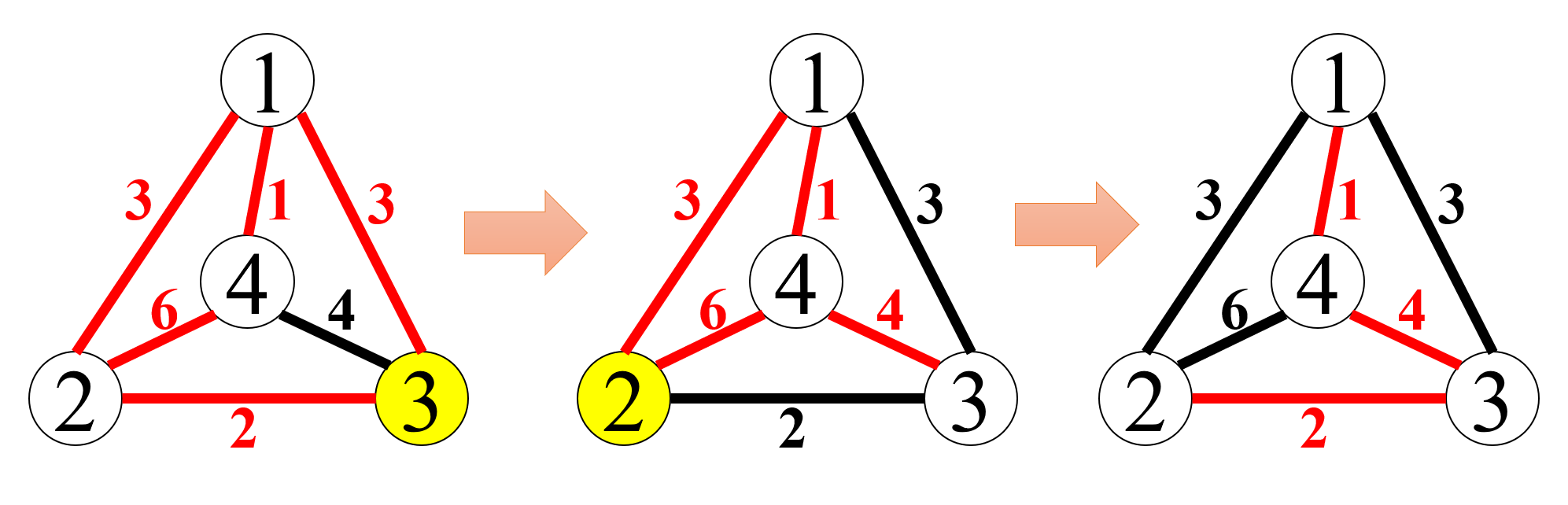
例として, 図 F-1 の左端のグラフはサンプル入力の最初のデータセットを図示したものである. 頂点 3 に繋がる全ての辺の色を反転し,次に頂点 2 に繋がる辺の色を反転することで, 図の右端に示すように赤の辺からなる全域木を構成することができる.
Input
入力は複数のデータセットからなる. 各データセットは次の形式で表される.
n
e1,2 e1,3 ... e1,n-1 e1,n
e2,3 e2,4 ... e2,n
...
en-1,n
整数 n (2 ≤ n ≤ 300) は頂点数を表す. 頂点には 1 から n までの番号がついている. 整数 ei,k (1 ≤ |ei,k| ≤ 105) は, 頂点 i と頂点 k を結ぶ辺のペナルティと初期状態での色を表す. 絶対値 |ei,k| は辺のペナルティを表す. ei,k > 0 のとき,頂点 i と頂点 k を結ぶ辺の色が初期状態で赤であることを, ei,k < 0 のとき黒であることを示す.
入力の終わりは,ゼロだけからなる行で表される. データセットの個数は 50 を超えない.
Output
各データセットに対し, 上述の操作で作れる赤い全域木のうちペナルティの合計が最小のものの値を出力せよ. 上述の操作では赤い全域木を作ることができないならば -1 を出力せよ.
Sample Input
4 3 3 1 2 6 -4 3 1 -10 100 5 -2 -2 -2 -2 -1 -1 -1 -1 -1 1 4 -4 7 6 2 3 -1 0
Output for the Sample Input
7 11 -1 9