凸多角形の加法

凸郎君は凸多角形が大好きである． 凸郎君は凸多角形を調べているうちに，以下の素敵な凸多角形の加法を思いついた．

xy 平面上の 2 点 (x₁, y₁) と (x₂, y₂) の和を (x₁ + x₂, y₁ + y₂) と定義する． 多角形を，その周上と内部の点すべての集合として扱う． このとき 2 つの多角形 S₁ と S₂ の和 S₁ + S₂ を v₁ ∈ S₁ および v₂ ∈ S₂ を満たす 2 点の和である点 v₁ + v₂ すべての集合と定義する． こう定義すると， 2 つの凸多角形の和が必ず凸多角形になるのだ! 非負の整数と多角形の積を， 0S = {(0, 0)} および正整数 k に対し kS = (k - 1)S + S と帰納的に定める． この問題では線分や一点も凸多角形であるとする．

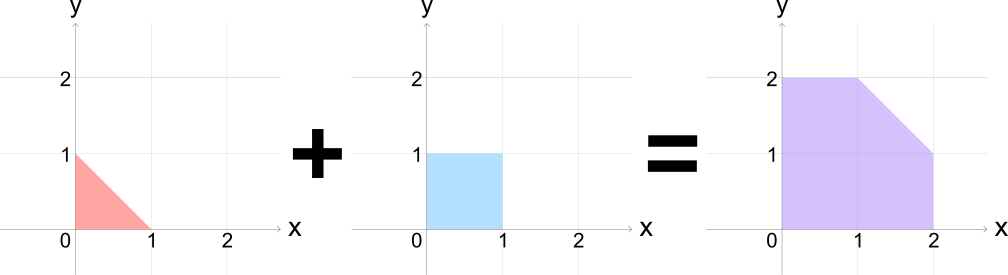
凸郎君はこの加法の性質を調べるため， 2 つの凸多角形 P と Q を基にたくさんの凸多角形を作ってみたが， ある日誤って元の多角形と計算過程を書いた紙を捨ててしまった． 手元に残ったのは P, Q の非負整数係数の線形結合:

R = aP + bQ,
S = cP + dQ,

で表される 2 つの凸多角形 R, S だけである． 幸いにも凸郎君は， P と Q のすべての頂点の座標が整数であることと，係数 a, b, c, d が ad - bc = 1 を満たしていることは覚えていた．

凸郎君は，プログラマーである友人のあなたに R と S から P と Q を復元するプログラムを依頼した． すなわち，凸多角形 R, S が与えられるので，非負の整数 a, b, c, d (ad - bc = 1) と頂点が整数座標の点であるような凸多角形 P, Q で 上の方程式を満たすものを求めてほしいというのである． この方程式は複数の解を持つかもしれない． 方程式を満たす P と Q の面積の和の最小値を求めるプログラムを作成せよ．

Input

入力は高々 40 個のデータセットからなる． 各データセットは次の形式で表される．

n m
x₁ y₁
...
x_n y_n
x'₁ y'₁
...
x'_m y'_m

n は凸多角形 R の頂点の個数を表し， m は凸多角形 S の頂点の個数を表す． n と m は整数であり，3 ≤ n ≤ 1000 および 3 ≤ m ≤ 1000 が成り立つ． (x_i, y_i) は凸多角形 R の i 番目の頂点の座標を表し， (x'_i, y'_i) は凸多角形 S の i 番目の頂点の座標を表す． x_i, y_i, x'_i, y'_i は，それぞれ整数であり −10⁶ 以上，10⁶ 以下である． 凸多角形 R, S の頂点はそれぞれ反時計回りの順番で与えられる． また，1 つの凸多角形の異なる 3 つの頂点は一直線上に並んでいない．

入力の終わりは，2 つのゼロからなる行で表される．

Output

各データセットについて，それぞれ 1 行に P と Q の面積の和の最小値を 2 倍した整数を出力せよ． P と Q の頂点の座標は整数なので，面積の 2 倍は常に整数となることに注意せよ．

Sample Input

5 3
0 0
2 0
2 1
1 2
0 2
0 0
1 0
0 1
4 4
0 0
5 0
5 5
0 5
0 0
2 0
2 2
0 2
3 3
0 0
1 0
0 1
0 1
0 0
1 1
3 3
0 0
1 0
1 1
0 0
1 0
1 1
4 4
0 0
2 0
2 2
0 2
0 0
1 0
1 2
0 2
4 4
0 0
3 0
3 1
0 1
0 0
1 0
1 1
0 1
0 0

Output for the Sample Input

3
2
2
1
0
2

---