Princess, a Strategist

お姫様は戦略家

English text is not available in this practice contest.

ある貧乏な国の勇敢なお姫様は，お城を抜け出して古の秘宝を手に入れる冒険に出かける算段をしている．ところが，古の秘宝の周囲は複数のガーディアンによって守られており，普通の方法では辿り着くことができない．そこで，お姫様は従者であるあなたを囮にし，ガーディアン達の注意を惹きつけている間に秘宝を取って来るという作戦を考えた．そのような事をされては命がいくつあっても足りない，しかしお姫様の命令に従わないわけにもいかない．そこで，まずあなたはあらかじめ偵察をし，どのように動けばガーディアンの攻撃をかわしつつ，注意を引きつけられるのかを念入りに調査した．あなたの仕事は，これらの調査結果をもとに囮であるあなたとガーディアンの発射する弾丸の衝突がいつ，そして何回起こったのか計算するプログラムを書くことである．

まず，簡単のため，フィールドとして十分に高い場所から見下ろした二次元平面を考える．そして，あなたはガーディアンの攻撃から身を守るために鎧を装備している．そのため，あなたの形は多角形でであるものと考えて良い．なお，この多角形の各線分は一切交差したり重なったりしない．また，あなたの移動については以下のことを仮定して良い．

• 等速直線運動しかしない．
  • 加速，減速，方向転換は全て一瞬で行われる．
  • 回転しないため向きは初期状態から一切変わらない．
• 多角形の全ての部分は常に y 座標が正の位置にある．

また，ガーディアンの発射する弾丸については，以下のことを仮定して良い．

• ガーディアンが発射する弾丸の太さは無視できる
• ガーディアンが発射する弾丸は有限の長さをもつ
• 長さ l の弾丸が先頭座標 (x, 0) から速度ベクトル (v_x, v_y) をもって発射されたとすると，弾丸の末尾座標は以下の地点にある（注：弾丸が発射される瞬間の弾丸の先頭の y 座標はすべて0である）：
  
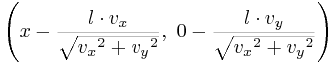
  • たとえば，(4, 0) の地点から速度ベクトル (3, 4) の長さ 10 の弾丸が発射されるケースでは弾丸の末尾は(-2, -8) にある
• 敵キャラクターが発射する弾丸同士の衝突は全て無視される

あなたとガーディアンの発射した弾丸の衝突の定義を以下に述べる．あなたを構成する多角形とガーディアンの発射する線分の共有点が初めて発生した時刻を弾丸の衝突時刻とする．ガーディアンの発射した弾丸にあなたが衝突したとしても，あなたはダメージを受けるだけで移動には何の支障もきたさないものとし，あなたに衝突した弾丸は衝突した瞬間に消滅するものとする．なお，あなたが初期位置から任意の方向に 10^-6 の範囲で平行移動したとしても，衝突時間は高々 10^-5 しか変化しないことが保証されている．

Input

入力は，複数のデータセットからなる．

それぞれのデータセットは，次のような形式で与えられる．

N M B
X₁ Y₁
...
X_N Y_N
T₁ VX₁ VY₁
...
T_M VX_M VY_M
T'₁ X'₁ VX'₁ VY'₁ L₁
...
T'_B X'_B VX'_B VY'_B L_B

各データセットの先頭には3つの非負整数 N (3 ≦ N ≦ 20)， M (0 ≦ M ≦ 100)， B (0 ≦ B ≦ 100) が与えられる． これらはそれぞれ，あなたである多角形の頂点の数，あなたの移動に関する情報の数，およびガーディアンの発射した弾丸の数を表す．

続く N 行では，あなたを表す多角形の頂点の時刻0での座標が順に列挙される． (X_i, Y_i) (1 ≦ i ≦ N) はそれぞれ，多角形の i 番目の頂点の座標を表す． これらの値はすべて整数であり， -10,000 ≦ X_i ≦ 10,000， 0 ＜ Y_i ≦ 10,000 を満たす．

続く M 行では， あなたの移動を表す指示が M 個与えられる． i番目 (1 ≦ i ≦ M) の移動指示は 3つの整数 T_i, VX_i, VY_i から成り立っており， これは 時刻 T_i-1 から T_i までの間，あなたの速度ベクトルを (VX_i, VY_i) に維持するということを意味する． ただし， 0 = T₀ ＜ T₁ ＜ T₂ ＜ ... ＜ T_M ≦ 10,000， -100 ≦ VX_i ≦ 100， -100 ≦ VY_i ≦ 100 である． あなたがすべての移動指示を終えた後（すなわち，時刻 T_M 以降）は移動を停止し， その場にとどまり続けるものとする． あなたが停止した以降にも弾丸との衝突が発生する可能性があり， 出力に際してはそのような衝突も考慮する必要があることに注意せよ．

続く B 行では，ガーディアンの発射する B 個の弾丸に関する情報が記述されている． i 番目 (1 ≦ i ≦ B) の弾丸に関する情報は5つの整数 T'_i， X'_i， VX'_i， VY'_i および L_i で表され，これは，時刻 T'_i に座標 (X'_i, 0) から速度ベクトル (VX'_i, VY'_i) をもつ長さ L_i の弾丸が発射されることを意味する． これらの値は 0 ≦ T'₁ ≦ T'₂ ≦ ... ≦ T'_B ≦ 10,000， -10,000 ≦ X'_i ≦ 10,000， -100 ≦ VX'_i ≦ 100， 0 ＜ VY'_i ≦ 100， 0 ＜ L_i ≦ 100 を満たす．

最後のデータセットの後ろに，データセットの終了を意味する "0 0 0" と書かれた1行が与えられる． これはデータセットの一部ではない．

Output

各データセットに対する出力の先頭に，あなたがガーディアンの発射した弾丸に衝突した回数 n を出力せよ．続く n 行では，あなたがガーディアンの発射した弾丸に衝突した時刻を昇順に誤差高々 0.001 の精度で出力せよ．

Sample Input

4 1 1
1 1
1 2
-1 2
-1 1
2 1 0
0 1 0 1 2
0 0 0

Output for the Sample Input

1
1.000

---