Grated Radish

Grated radish (daikon-oroshi) is one of the essential spices in Japanese cuisine. As the name shows, it’s made by grating white radish.

You are developing an automated robot for grating radish. You have finally finished developing mechan- ical modules that grates radish according to given instructions from the microcomputer. So you need to develop the software in the microcomputer that controls the mechanical modules. As the first step, you have decided to write a program that simulates the given instructions and predicts the resulting shape of the radish.

Input

The input consists of a number of test cases. The first line on each case contains two floating numbers R and L (in centimeters), representing the radius and the length of the cylinder-shaped radish, respectively. The white radish is placed in the xyz-coordinate system in such a way that cylinder’s axis of rotational symmetry lies on the z axis.

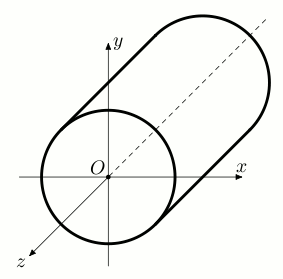
Figure 1: The placement of the white radish

The next line contains a single integer N, the number of instructions. The following N lines specify instructions given to the grating robot. Each instruction consists of two floating numbers θ and V, where θ is the angle of grating plane in degrees, and V (in cubic centimeters) is the volume of the grated part of the radish.

You may assume the following conditions:

• the direction is measured from positive x axis (0 degree) to positive y axis (90 degrees),
• 1 ≤ R ≤ 5 (in centimeters),
• 1 ≤ L ≤ 40 (in centimeters),
• 0 ≤ θ < 360, and
• the sum of V’s is the smaller than the volume of the given white radish.

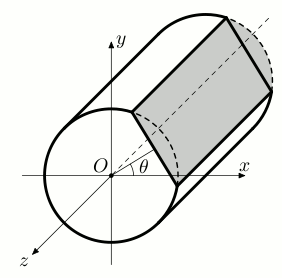
Figure 2: An example of grating

Output

For each test case, print out in one line two numbers that indicate the shape of the base side (the side parallel to xy-plane) of the remaining radish after the entire grating procedure is finished, where the first number of the total length is the linear (straight) part and the second is the total length of the curved part.

You may output an arbitrary number of digits after the decimal points, provided that difference from the true answer is smaller than 10^-6 centimeters.

Sample Input

2
1 2
1
42 3.141592653589793
5 20
3
0 307.09242465218927
180 307.09242465218927
90 728.30573874452591

Output for the Sample Input

2.0 3.141592653589793
8.660254038 5.235987756

---