Problem G:エナジー・トランスポーター
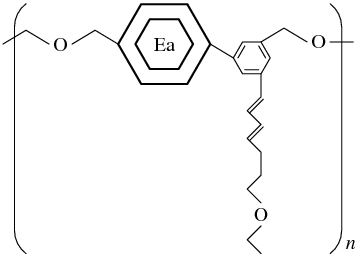
とある研究所で, エネルギー伝達用の媒体の開発をしていた. この媒体は図3に示すような特殊な物質からなる ポリマー構造をなしている.
|
| (-α-Ea-β-)n |
| 図3: エネルギー伝達用媒体の構造. |
図の Ea で示した部分がこの媒体のもっとも特徴的な部位の エナジーアキュムレータ (Energy Accumulator) である. このEa基は 1 kJ 幅で離散化された多様なエネルギー状態を取ることができる. あるEa基を励起させると, そのEa基のα側に結合している隣接したEa基に蓄積されている全エネルギーを β側に結合している隣接したEa基に移動させるような効果を持つ 発熱反応が引き起こされる(図4). この反応の際,励起されるEa基のエネルギーが 1 kJ 消費される. なお,ポリマーの両端に位置するEa基やエネルギー状態が 0 kJ になっている Ea基に対しては励起反応は発生しないこと, およびEa基は十分に大きなエネルギーを蓄えることが可能であることが知られている.
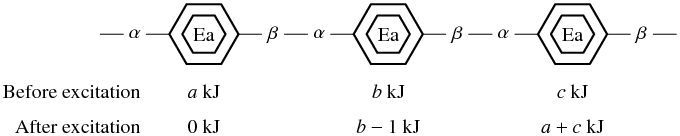
|
| 図4: 中央のEa基を励起させたときの反応. |
この性質を利用することでエネルギーの伝達を可能にしようと考えていたのだが, エネルギーを効率よく伝達するには各Ea基を励起させる順番が重要であることに 研究者たちは気がついたのである.
幸い,励起させる順番や回数は任意に制御できるのだが, 彼らには最適な励起手順がわからない. そこで彼らの発想の足がかりとして, 初期状態のエネルギー分布に対して 最右Ea基(β末端からもっとも近いEa基) に蓄えられうる最大のエネルギー量を計算してもらいたい.
Input
入力は複数のデータセットから構成され, 以下のような形式で与えられる.
N
C1
C2
...
CN
入力の先頭の整数 N (0 < N ≤ 60) が取り扱う問題のデータセット数であり, その後ろ 2N 行に渡って, それぞれのデータセットごとの情報 Ck が与えられる.
それぞれのデータセット Ck は以下のような形式で 2行に渡り与えられる.
L
E1 E2 ... EL
L はそれぞれのデータセットで取り扱う媒体のEa鎖の長さであり, ここで与えられた数だけEa基が直列に結合していることを意味している. その次の行の L 個の整数 Ek は, 長さLのEa鎖のうちα末端を左端に据えたときに 左から数えてk番目のEa鎖にはじめに蓄積されているエネルギー量を kJ単位で示したものである.
ここで, 0 ≤ Ek ≤ 4, 1 ≤ L ≤ 80 であることが保証されている.
Output
出力は各データセットごとに,与えられた状況下での右端Ea鎖に到達可能な 最大エネルギーをkJ単位で,整数値のみを1行で記述すること.
Sample Input
7 1 2 2 1 2 3 4 1 4 3 4 0 4 5 4 1 4 0 4 5 4 1 4 1 4 5 4 2 4 0 4
Output for the Sample Input
2 2 8 4 7 12 11