Problem B: Left Hand Rule
The left-hand rule, which is also known as the wall follower, is a well-known strategy that solves a two- dimensional maze. The strategy can be stated as follows: once you have entered the maze, walk around with keeping your left hand in contact with the wall until you reach the goal. In fact, it is proven that this strategy solves some kind of mazes.
Your task is to write a program that determines whether the given maze is solvable by using the left-hand rule and (if the maze is solvable) the number of steps to reach the exit. Moving to a cell from the entrance or the adjacent (north, south, east or west) cell is counted as a step.
In this problem, the maze is represented by a collection of walls placed on the two-dimensional grid. We use an ordinary Cartesian coordinate system; the positive x-axis points right and the positive y-axis points up. Each wall is represented by a line segment which is parallel to the x-axis or the y-axis, such that both ends of each wall are located on integer coordinates. The size of the maze is given by W and H that indicate the width and the height of the maze, respectively. A rectangle whose vertices are on (0, 0), (W, 0), (W, H) and (0, H) forms the outside boundary of the maze. The outside of the maze is always surrounded by walls except for the entrance of the maze. The entrance is represented by a line segment whose ends are (xE, yE) and (xE', yE'). The entrance has a unit length and is located somewhere on one edge of the boundary. The exit is a unit square whose bottom left corner is located on (xX, yX).
A few examples of mazes are illustrated in the figure below. They correspond to the datasets in the sample input.
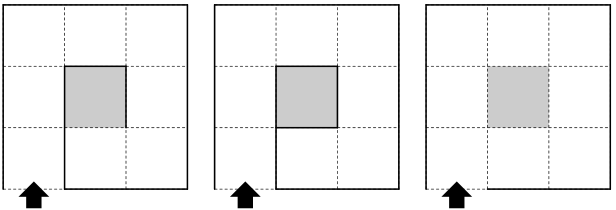
Figure 1: Example Mazes (shaded squares indicate the exits)
Input
The input consists of multiple datasets.
Each dataset is formatted as follows:
W H N
x1 y1 x1' y1'
x2 y2 x2' y2'
...
xN yN xN' yN'
xE yE xE' yE' xX yX
W and H (0 < W, H ≤ 100) indicate the size of the maze. N is the number of walls inside the maze. The next N lines give the positions of the walls, where (xi, yi) and (xi', yi') denote two ends of each wall (1 ≤ i ≤ N). The last line gives the positions of the entrance and the exit. You can assume that all the coordinates given in the input are integer coordinates and located inside the boundary of the maze. You can also assume that the wall description is not redundant, i.e. an endpoint of a wall is not shared by any other wall that is parallel to it.
The input is terminated by a line with three zeros.
Output
For each dataset, print a line that contains the number of steps required to reach the exit. If the given maze is unsolvable, print “Impossible” instead of the number of steps.
Sample Input
3 3 3 1 0 1 2 1 2 2 2 2 2 2 1 0 0 1 0 1 1 3 3 4 1 0 1 2 1 2 2 2 2 2 2 1 2 1 1 1 0 0 1 0 1 1 3 3 0 0 0 1 0 1 1 0 0 0
Output for the Sample Input
9 Impossible Impossible