Problem I: Lapin Noir
ここは, 地面が正六角形を敷き詰めたマス目になっている街である. 各マスは, 下の図のように2 つの整数で表される.
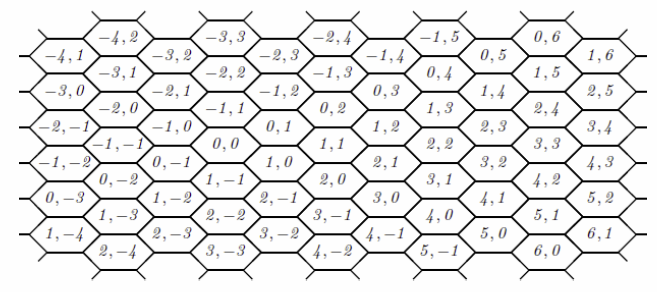
ねこは(0, 0) のマスへ行こうとしている. いたずら好きの黒うさぎはこのことを知って, ねこの邪魔をしようと考えた.
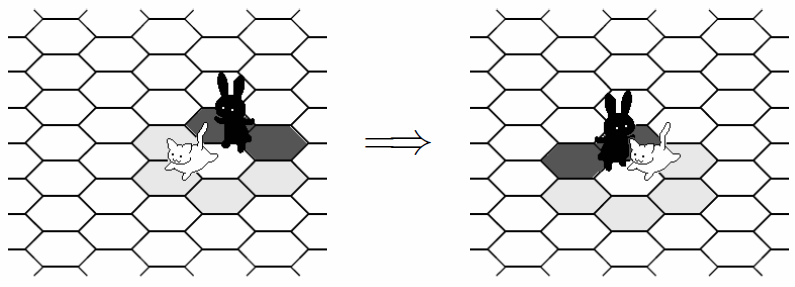
黒うさぎはねこがいるマスへ跳び, その周りの6 マスのうち1 つまたは隣り合う2 つをブロックすることができる. ねこは周りの6 マスのうち, ブロックされていないマスを1 つ選んで進む. ねこが動くたび黒うさぎはねこを追いかけ, またブロックを行うことができる. 黒うさぎが動くと元のブロックは解除される. 下の図はブロックの様子を示している.
この街にはねこの縄張りとなっているマス目がいくつかある. 縄張りは正六角形の周をなすマス目の集合n個の合併として表される. 黒うさぎはねこの縄張りに立ち入ることはできるが, ブロックすることはできない.つまり, ねこは縄張り内であれば自由に動ける.
ねこの出発点の候補がk 個あり, マス(xi, yi) (1 ≤ i ≤ k) である. それぞれについて, ねこが必ず目的地(0, 0) に辿り着けるか, あるいは黒うさぎがうまく妨害することによってねこが目的地に辿り着けないかを判定せよ.
Input
1 行目:1 ≤ n ≤ 40 000
2 ∼ (n + 1) 行目: ねこの縄張りを表す正六角形の頂点
(n + 2) 行目: 1 ≤ k ≤ 40 000
(n + 3) ∼ (n + k + 2) 行目: ねこの出発点xi, yi
−1 000 000 000 ≤ (各座標) ≤ 1 000 000 000
ねこの縄張りを表す正六角形は, 6 頂点の位置が反時計回りに与えられる.
Output
出発地の候補それぞれについて, ねこが必ず目的地(0,0) に辿り着けるなら”YES”を, あるいは黒うさぎがうまく妨害した場合ねこが目的地に辿り着けないなら”NO”を, 一行ずつ出力せよ.
Sample Input 1
2 1 -1 3 -1 3 1 1 3 -1 3 -1 1 3 0 4 0 4 1 3 2 2 2 2 1 3 1 1 -1 -1 2 4
Sample Output 1
YES NO YES