Problem B: Step Step Evolution

Japanese video game company has developed the music video game called Step Step Evolution. The gameplay of Step Step Evolution is very simple. Players stand on the dance platform, and step on panels on it according to a sequence of arrows shown in the front screen.

There are eight types of direction arrows in the Step Step Evolution: UP, UPPER RIGHT, RIGHT, LOWER RIGHT, DOWN, LOWER LEFT, LEFT, and UPPER LEFT. These direction arrows will scroll upward from the bottom of the screen. When the direction arrow overlaps the stationary arrow nearby the top, then the player must step on the corresponding arrow panel on the dance platform. The figure below shows how the dance platform looks like.

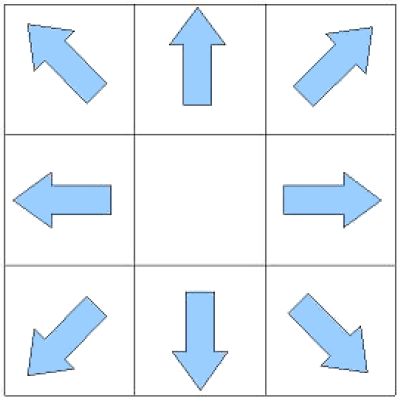
Figure 1: the dance platform for Step Step Evolution

In the game, you have to obey the following rule:

• Except for the beginning of the play, you must not press the arrow panel which is not correspond to the edit data.
• The foot must stay upon the panel where it presses last time, and will not be moved until it’s going to press the next arrow panel.
• The left foot must not step on the panel which locates at right to the panel on which the right foot rests. Conversely, the right foot must not step on the panel which locates at left to the panel on which the left foot rests.

As for the third condition, the following figure shows the examples of the valid and invalid footsteps.

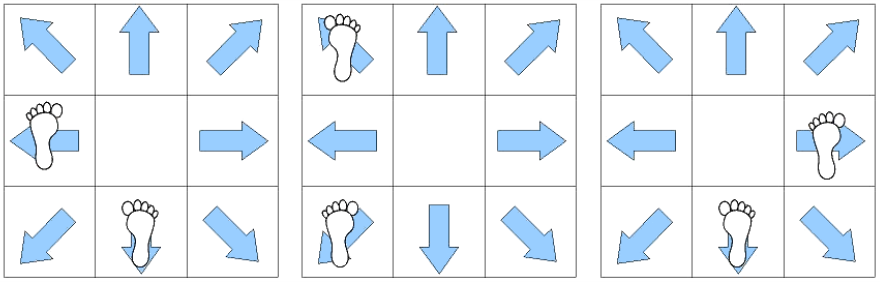
Figure 2: the examples of valid and invalid footsteps

The first one (left foot for LEFT, right foot for DOWN) and the second one (left foot for LOWER LEFT, right foot for UPPER LEFT) are valid footstep. The last one (left foot for RIGHT, right foot for DOWN) is invalid footstep.

Note that, at the beginning of the play, the left foot and right foot can be placed anywhere at the arrow panel. Also, you can start first step with left foot or right foot, whichever you want.

To play this game in a beautiful way, the play style called “ Natural footstep style” is commonly known among talented players. “Natural footstep style” is the style in which players make steps by the left foot and the right foot in turn. However, when a sequence of arrows is difficult, players are sometimes forced to violate this style.

Now, your friend has created an edit data (the original sequence of direction arrows to be pushed) for you. You are interested in how many times you have to violate “Natural footstep style” when you optimally played with this edit data. In other words, what is the minimum number of times you have to step on two consecutive arrows using the same foot?

Input

The input consists of several detasets. Each dataset is specified by one line containing a sequence of direction arrows. Directions are described by numbers from 1 to 9, except for 5. The figure below shows the correspondence between numbers and directions.

You may assume that the length of the sequence is between 1 and 100000, inclusive. Also, arrows of the same direction won’t appear consecutively in the line. The end of the input is indicated by a single “#”.

Figure 3: the correspondence of the numbers to the direction arrows

Output

For each dataset, output how many times you have to violate “Natural footstep style” when you play optimally in one line.

Sample Input

1
12
123
369
6748
4247219123
1232123212321232
#

Output for the Sample Input

0
0
1
0
1
2
7

---