問題 J : 乱択平衡分二分探索木
ところで,G○○gle Code Jam の地区大会で右の席に座っていた男の ID は rng_58 と言うらしい. 東京大学時代の記憶に,似たような ID の仲間が居た覚えがあるが,僕の仲間は一人残さず美少女だったはずだ. 彼女はいわゆる無表情不思議系キャラだったような気がする.
ということは,彼は知らない男だ.rng とは何の略だろう. おそらく Random Number Generator に違いない. 乱択アルゴリズムを得意とするのだろう.
ところで,乱数を用いた平衡二分探索木である Treap は, 2011 年頃のプログラミングコンテストではしばしば用いられていたようだが, 20XX 年の今では,あまり使用されていない.
当時 Treap は実装が平易であるという理由により Splay 木や Scapegoat 木と並んでよく使われていた. 20XX 年の今,命をかけたプログラミングコンテストが日常的に行われるこの世界では, 実装が多少平易になるというような甘い根拠での選択は到底考えられない. 皆,少しでもプログラムが高速になるよう考えているし, 世界大会出場者ともなれば,Left-leaning 赤黒木程度なら十数秒で記述できるのが当然だ.
例えば,Treap が赤黒木よりも遅くなってしまうのは, 高さの定数倍が効いてくるからであると言われている. ここは,落ち着いてそれを数値的に考察することにより,精神の安定を取り戻そう.
問題
キーを実数とする Treap に N 個のランダムな要素を挿入した際に, 高さが h (h = 0, 1, …, N - 1) となる確率を求めよ. 以下,より詳しく説明する.
Treap とは乱数を用いた平衡二分探索木である. 各ノードは,キーの他に,優先度という値を持つ. ここでは,キーと優先度は 0 から 1 までの実数値とする. Treap では,以下の 2 つの条件が常に保たれる.
- キーに関する条件
- 各ノードに関して,左の子以下のノードは自分より小さなキーを持つ
- 各ノードに関して,右の子以下のノードは自分より大きなキーを持つ
- 優先度に関する条件
- 各ノードに関して,子のノードは自分より小さな優先度を持つ
下図は,Treap の例である. 各ノードの,上部にキーが,下部に優先度が書かれている.
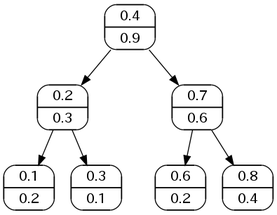
7 つのノードからなる Treap の例.
挿入の操作は,以下のように行われる. 挿入するキー を x とおく.
- 挿入する新しいノードの優先度 p を 0 から 1 までの一様分布よりランダムに決定する.
- 通常の二分探索木と同様に,まずは優先度を無視し新しいノードを挿入する.
- 優先度の条件を満たすように,新しいノードを上に持ち上げるような回転操作を必要なだけ繰り返す.
木の回転操作に関しては,補足の節に詳しく記述したので,参考にせよ.
下図は,先ほどの例にキーとして 0.5,優先度として 0.7 を持つ頂点を挿入した過程の例である.
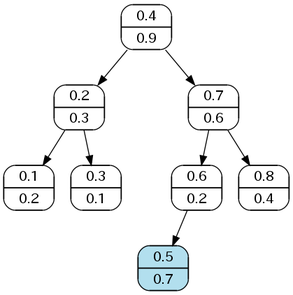
まずは優先度が無視され,ノードが挿入される.
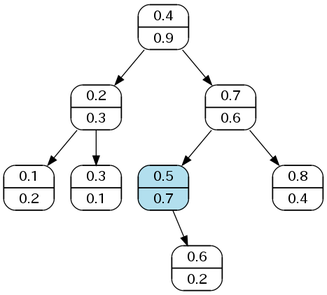
回転を行い新しいノードが上へ行く.
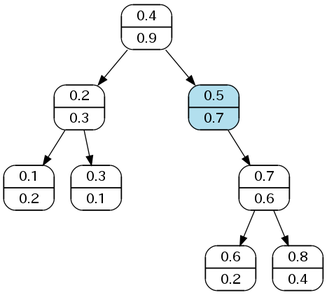
さらに回転を行うと,優先度の条件が満たされるので,挿入は終了する.
空の Treap に N 個のキーを, やはり 0 から 1 までの一様分布よりランダムに選び挿入してゆくとする. 最終的に高さが h となる確率を, 各 h = 0, 1, …, N - 1 について求めよ. なお,実数は十分な精度を持って扱われるとし, 例えば 2 つのノードの優先度が等しくなる確率は 0 としてよい. また,高さとは,根のノードから各ノードに至るために通らなければならない辺の本数の最大値である.
入力
1 つの整数 N が書かれている.
出力
出力は N 行から成る. i 行目に高さが i - 1 となる確率を出力せよ. 値は小数点以下何桁表示しても構わない.
制約
- 1 ≤ N ≤ 3 × 104
- 出力する値は 10 - 5 以下の誤差を含んでいても構わない.
入出力例
入力例 1:
1
入力例 1 に対する出力例:
1.0
入力例 2:
2
入力例 2 に対する出力例:
0.0000000000 1.0000000000
補足
木の回転操作には,右回転と左回転がある. 右回転とは,以下の 2 つの図の 1 つめの状態を 2 つめの状態にする操作であり, 左回転とは,以下の 2 つの図の 2 つめの状態を 1 つめの状態にする操作である.
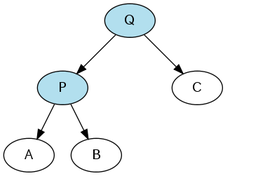
右回転をする前,または左回転をした後
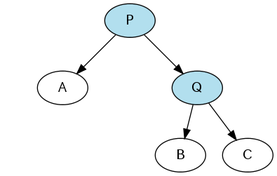
右回転をした後,または左回転をする前
Treap においては,持ち上げたいノードがその親ノードの左の子であった場合, 持ち上げたいノードを上図の P とするような右回転を適用し, 持ち上げたいノードがその親ノードの右の子であった場合, 持ち上げたいノードを上図の Q とするような左回転を適用する.
木の回転操作について,より詳しくは,例えば以下を参照せよ.
Treap について,より詳しくは,例えば以下を参照せよ.