Problem F: 10歳の動的計画
ある日の夕方。いつものようにあなたが居間でテレビを見ていると、小学5年生の妹から相談を持ち かけられた。話を聞いてみると、今日学校で出された算数の問題が難しくて理解できなかったので、 あなたに解き方を教えてほしいのだという。
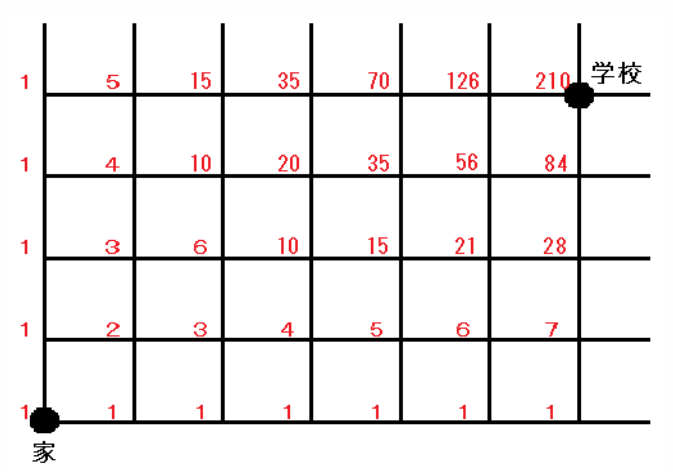
妹を悩ませている問題は、「道が碁盤目状に通っている街において、家(0, 0) から学校(N, M) まで最短距離で進む方法は何通りあるか?」というものだった。もちろん、あなたにとっては赤子の手をひねるよりも簡単な問題である。すぐに上のような図を書いて「家(0, 0) から順番に足し算していけば解けるよ」と教えてあげた。
ところが、それを聞いてもまだ、妹はなにやら下を向いて考えこんでいる。あなたは、自分の説明の 仕方が悪かったのだろうかと思ったが、どうやらそうではないらしい。
たっぷり3分ほど悩んでいただろうか。妹は、おもむろに顔を上げると、あなたに向かってこう言っ た。
「でも、わたしだったら、きっと学校に行く途中でK 回くらい寄り道しちゃうだろうな……。ねぇお 兄ちゃん、そうすると答えは何通りになるの?」
さあ大変だ。兄の威厳を保つため、なんとしてもこの問題に答えねば。
この問題を定式化すると、次のようになる。
- 点(0, 0) から点(N, M) まで、碁盤目状の道を通って進む方法は何通りあるか答えよ。
- 基本的には右か上に1マス進むが、途中で、ちょうどK 回だけ寄り道をする。
- 「寄り道をする」とは、左か下に1マス進むことである。
- K 回の寄り道をすませていない場合、いったん点(N, M) に着いた後でも歩き続ける。途中で点(0, 0) に戻ってくる場合もある。
- 家はこの街の隅に建っているので、X 座標またはY 座標が負になるような点に入ることはできない。
- しかし、X 座標がN より大きな点、または、Y 座標がM より大きな点には入ることができる。
Input
N M K
入力の1行目には、整数N(1 ≤ N ≤ 100,000)と整数M(1 ≤ M ≤ 100,000)と整数K(0 ≤ K ≤ 10,000)が、この順に空白区切りで書かれている。整数N は学校のX 座標を、整数M は学校のY座標を、整数K は寄り道の回数をあらわす。
Output
点(0, 0) から点(N, M) まで、K 回の寄り道をして進む方法。その総数を1,000,000,007 で割った余りを出力せよ。なお1,000,000,007 は素数である。
Sample Input 1
6 4 0
Sample Output 1
210
Sample Input 2
3 3 1
Sample Output 2
448
Sample Input 3
124 218 367
Sample Output 3
817857665