問題文
1つの陰関数 $Ax^2+Bxy+Cy^2+Dx+Ey+F=0$ で与えられる曲線と、 $N$ 個の陰関数 $A_ix+B_iy+C_i=0$ で与えられる直線がある。 これらの曲線と直線によって平面がいくつの領域に分割されているか求めよ。
以下はSample Inputのデータセットを図示したものである。
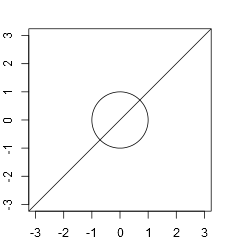
入力
入力は以下の形式に従う。与えられる数は全て整数である。
$N$ $A$ $B$ $C$ $D$ $E$ $F$ $A_1$ $B_1$ $C_1$ $...$ $A_N$ $B_N$ $C_N$
制約
- $1 \leq N \leq 20$
- $-100 \leq A,B,C,D,E,F \leq 100$
- $-100 \leq A_i,B_i,C_i \leq 100$
- $A_i \neq 0$ または $B_i \neq 0$
- 曲線は楕円(正円を含む)、放物線、双曲線のいずれかである。
- 同一の直線が存在する場合がある。
出力
領域の数を1行に出力せよ。
Sample Input 1
1 1 0 1 0 0 -1 1 -1 0
Output for the Sample Input 1
4
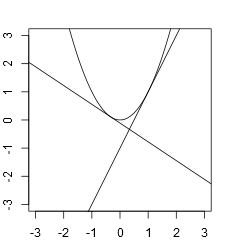
Sample Input 2
2 1 0 0 0 -1 0 2 -1 -1 6 9 1
Output for the Sample Input 2
7
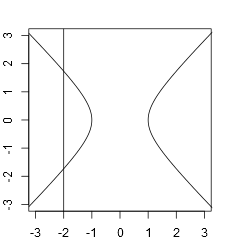
Sample Input 3
2 1 0 -1 0 0 -1 3 0 6 -5 0 -10
Output for the Sample Input 3
6