Problem J: Top of the Hill

You are participating in a radio control car race. The car is so easy to operate that you can navigate the car wherever you want it to go.

In the race, the contestants drive their cars on a large, flat stage with N cylindrical discs on it. Some discs are lying on another disc but no disc runs off the edge of the disc underneath. All cylindrical discs has the same height (or, "thickness".) All edges of discs never touch or intersect each other.

The car is secure enough that it can get off a disc by just falling down vertically from any point on its edge, but it has to use elevator to get on a disc. There are four elevators at north, south, east and west side of each disc.

Initially, the car is at $(cx, cy)$, and a goal is the highest point on the stage. If there are many points, you can choose any one of them.

You really want to win the race, so you decided to write a program to calculate the shortest distance your car has to run from the start to the goal. The car is not running while the car is getting on or off the discs, so you don't have to sum up the height of discs.

The figure below shows an example of the shortest path from the start to the goal.

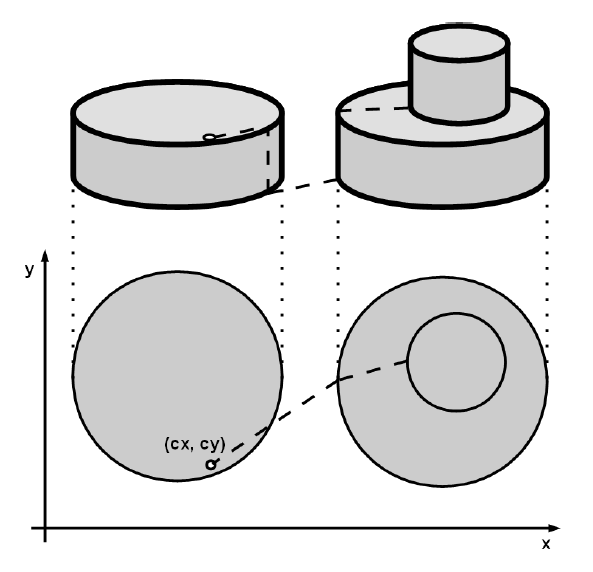
Note that the car is small enough that you can ignore its width.

Input

The first line of the input contains one integer $N$ ($1 \leq N \leq 30$), the number of cylindrical discs. The next line contains two integers $cx, cy$ ($|cx|, |cy| \leq 100$) which describe the initial coordinates of a radio control car. Then each of the following $N$ lines consists of three integers $x_i$, $y_i$, $r_i$ ($|x_i|, |y_i| \leq 100, 1 \leq r_i \leq 100$), where ($x_i$, $y_i$) is the coordinates of the center of the $i$-th disc and $r_i$ is its radius respectively. You can assume that the initial point of the radio control car is not on boundaries of any discs.

Output

Output the shortest distance the car should run. The absolute error should be less than or equal to $10^{-6}$.

Sample Input 1

1
0 0
10 10 10

Sample Output 1

10.0

Sample Input 2

3
5 5
0 0 1
0 0 2
3 3 2

Sample Output 2

7.242640687

Sample Input 3

3
30 10
25 15 10
50 15 10
52 17 2

Sample Output 3

21.378378914

---