最長増加列問題

時は過ぎて太郎君は高校生になりました。 大学生だったお兄さんの影響も受け、コンピューターサイエンスに興味を持ち始めました。 太郎君はコンピューターサイエンスの教科書を読み進め、「最長増加部分列問題」という有名問題があることを知りました。太郎君はこの問題のことを理解しましたが、自分でも類似問題が作れないものかと気になりました。 そこで太郎君は試行錯誤の結果に次のような問題を作りました。

• n個の整数で構成される数列Aがある
• m-1個の区切りを入れて、数列Aをm個の数列に分解する。なお、分解後のそれぞれの数列は1つ以上の数を必ず含まなければならない。
• このm個それぞれの数列内の整数をすべて足し合わせた結果出来上がるm個の数を、元の数列の順に配置すると厳密な増加列になっている(つまり、出来上がる数列はB_i < B_i+1をみたす)ようにしたい。
• 目標は最終的にできる数列Bの長さmを最大化することである。

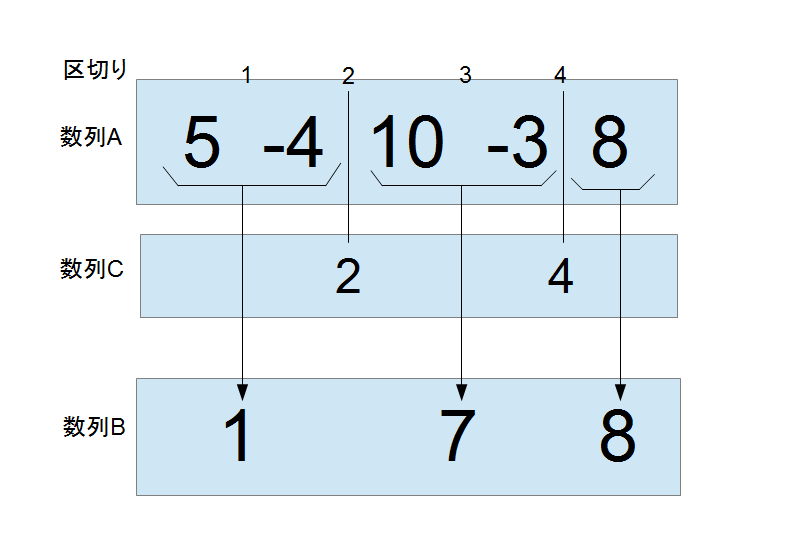
例えば、数列Aが{5,-4,10,-3,8}の場合を考えてみる。
区切りの位置を表す数列Cを用意し、C={2,4}とする。
このとき、数列Aは(5,-4),(10,-3),(8)の部分に分かれ、これらの内部を足し合わせるとそれぞれ1,7,8となり、出来上がる数列Bは{1,7,8}となる。

太郎君はこの問題について"最長増加列問題"と名付け、これを解くアルゴリズムも考えました。
そして社会人になったあなたにチェックをしてほしいと連絡をしました。 あなたの仕事は、成長した太郎君の作った問題を解くプログラムを作ることです。
チェックするのが仕事なので、m-1個の区切りの位置も出力します。 なお、最適なmに対してこのような区切り方が複数考えられる場合もありますが、このmが正しく出力されていれば、考えられるもののうち一つを出力すればよいです。

Input

改行区切りでn+1個の整数が与えられる。

n
A₁
A₂
...
A_n

• nは与えられる数列Aの長さを表す
• A_iは数列Aのi番目の要素を表す。

Constraints

1≤n≤4000
|Ai|≤ 10⁸　

• 整数kに対して|k|はkの絶対値を表す

Output

m
C₁ C₂ .. C_m-1

• 1行目は一つの整数mを出力する。 mは最終的にできる数列Bの長さを表す。 2行目はm-1個の整数C_iを空白区切りで出力する。 C_iは、数列Aをm個の部分に適切に区切った時のi番目の区切り場所を表す。 区切り場所の定義は図を参照せよ。なお、1≤C_i<n を満たす。 2行目のm-1個の整数列Cは昇順に並んでいなければならないしたがって、i < j ならば C_i < C_j が成立する。

• m=1の場合2行目は空行になる。
• 数列Cに従って数列Aから数列Bを生成したとき、数列Bが増加列になっていないとき(すなわちB_i≥B_i+1となるi(1≤i<m)が存在するとき)、WrongAnswerとなる

Sample Input 1

3
1
2
4

Output for the Sample Input 1

3
1 2

もともと増加列なので、すべての場所に区切りを入れればよい

Sample Input 2

3
2
2
2

Output for the Sample Input 2

2
1

2 2 2は増加列でないので、3つに分割することはできない

Sample Input 3

3
4
2
1

Output for the Sample Input 3

1
(空行)

どう分割しても増加列にはならないため、分割をしない

---