Convex-Cut

N個の頂点からなる凸多角形が与えられる。各頂点の座標は反時計周りに(X₁, Y₁), (X₂ ,Y₂), ……, (X_N, Y_N)で表わされる。 点Pを通るどのような直線で凸多角形を切断しても、切断後に得られる2つの凸多角形の面積が等しいような点Pの座標を求めよ。

Input

入力は以下の形式で与えられる。

N
X₁ Y₁
X₂ Y₂
……
X_N Y_N

Constraints

• 入力は全て整数である

• 3 ≤ N ≤ 50

• 0 ≤ |X_i|, |Y_i| ≤ 1000000

• 入力の多角形は単純な凸多角形である。

• 出力は、出力座標を(X, Y)、厳密解を(cX, cY)とした時にmax(|X-cX|, |Y-cY|) ≤ 0.0001を満たす必要がある

Output

問題文の条件を満たす点があるのならば、その点の座標を

X Y

の形式で出力せよ。 点が存在しない場合は"NA"と1行に出力せよ。

Sample Input 1

4
100 100
0 100
0 0
100 0

以下の図に対応する。

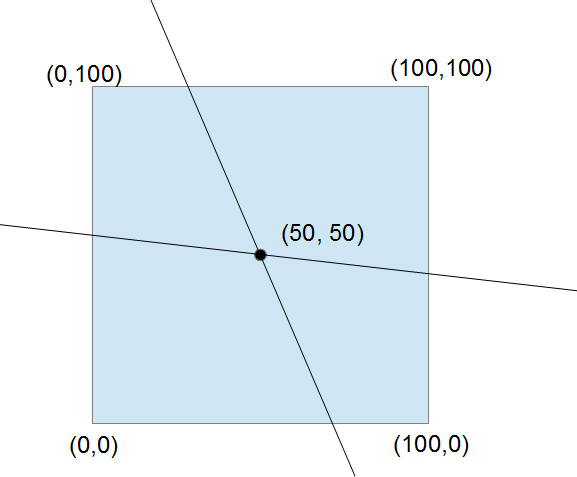
Output for the Sample Input 1

50.00000 50.00000

Sample Input 2

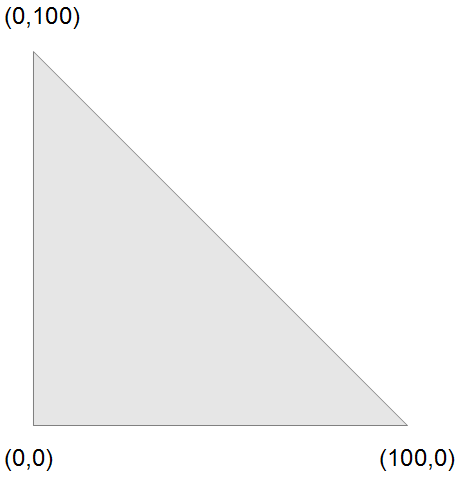
3
100 100
0 100
0 0

Output for the Sample Input 2

NA

以下の図に対応する。

---