MinimumCostPath

NxNの方眼がある。

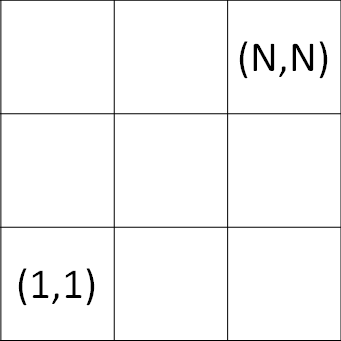
(N=3の場合の図)

隣接するマス目に移動するにはコストが1かかる。ただし、斜めに移動することは出来ない。 また障害物があるマス目がM個あり、そのマスに入ることは許されない。 マス(1, 1)からマス(N, N)に最小のコストで移動する方法は何通りあるか。 答えは大きくなることがありうるので、1000000009(=10⁹+9)でMODを取って出力せよ。

Input

入力は以下の形式で与えられる

N M
X₁ Y₁
X₂ Y₂
……
X_M Y_M

X_i, Y_iは(X_i, Y_i)に障害物があることを表す

Constraints

• 2 ≤ N ≤ 10⁶

• 0 ≤ M ≤ 50

• 1 ≤ X_i , Y_i ≤ N

• i ≠ jならば (X_i, Y_i) ≠ (X_j, Y_j)

• (X_i, Y_i) ≠ (1, 1)

• (X_i, Y_i) ≠ (N, N)

Output

1行に経路の総数を出力せよ。ただし、マス(1, 1)からマス(N, N)に移動する経路が存在しない場合は0と出力せよ。

Sample Input 1

3 0

Output for the Sample Input 1

6

以下の図に対応する。

Sample Input 2

3 1
2 2

Output for the Sample Input 2

2

以下の図に対応する。

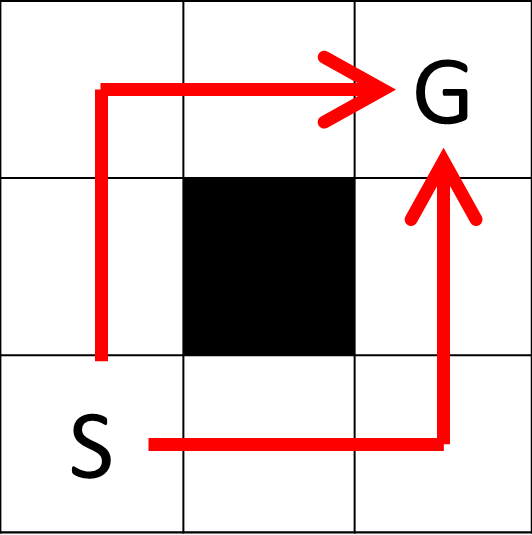
Sample Input 3

5 8
4 3
2 1
4 2
4 4
3 4
2 2
2 4
1 4

Output for the Sample Input 3

1

以下の図に対応する。

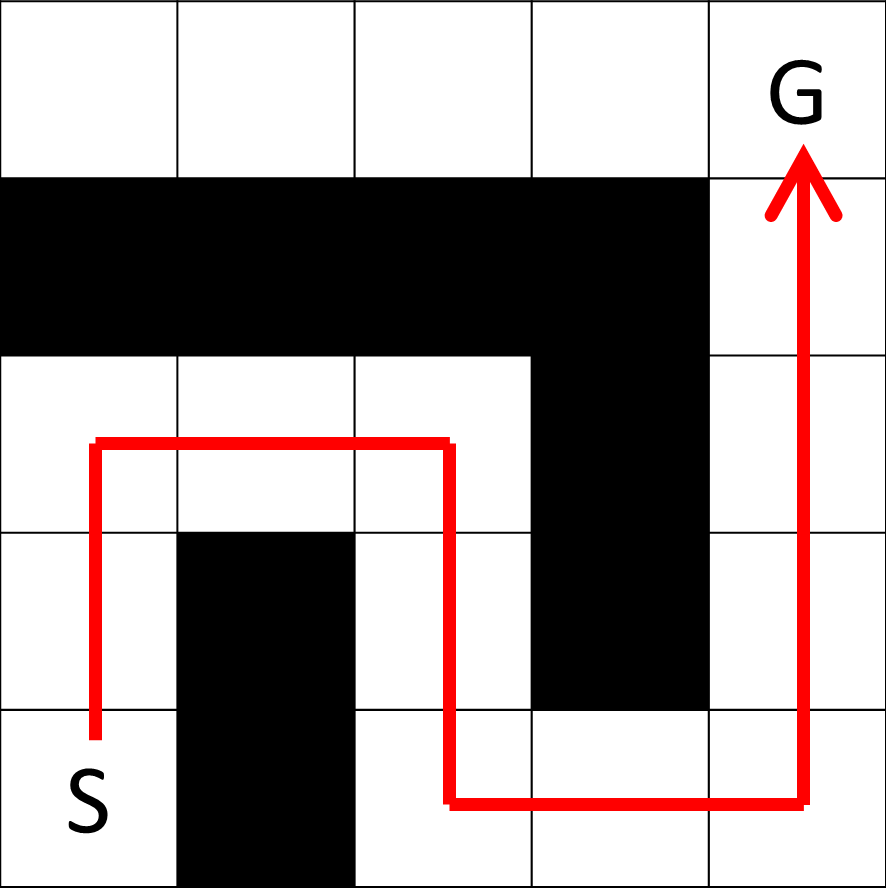
Sample Input 4

1000 10
104 87
637 366
393 681
215 604
707 876
943 414
95 327
93 415
663 596
661 842

Output for the Sample Input 4

340340391

Sample Input 5

2 2
1 2
2 1

Output for the Sample Input 5

0

---