Move On Dice

There is a cube on a rectangle map with H-rows and W-columns grid. Two special squares a start and a goal are marked on the map. Initially, the cube is on the start square. Let's repeat to roll it and take it to the goal square. Rolling the cube means to select one of four edges which touch the map, and push the cube down without detaching the edge from the map. That is, there are four directions you can move the cube toward.

Directions where we can roll the cube are limited depending on each square. An instruction is written in each square and represented by a single character as follows:

'+'

all

'|'

only vertical

'-'

only horizontal

'<'

only to left

'>'

only to right

'^'

only to up

'v'

only to down

'.'

none

Regardless of instructions, it is not allowed to roll the cube to outside of the map.

On each face of the cube, a string is written. Let's output the string which concatenates strings written on the top face seen during the rollings from the start square to the goal square. Since there may be multiple paths that take the cube to the goal square, choose the minimal string in ascending lexicographic order.

Please note that there are cases where no path exists from the start to the goal, or the cases you can make the lexicographically minimal string infinitely longer.

Input

A data set has following format:

H W
C₁₁ ... C_1W
...
C_H1 ... C_HW
T₁
...
T₆
R_S C_S
R_D C_D

The first line of the input contains two integers H (1 ≤ H ≤ 12) and W (1 ≤ W ≤ 12), which indicate the number of rows and columns of the map respectively. The following W lines describe the map. The j-th character of the i-th line indicates the instruction of the square, which is placed on i-th row (from the top) and j-th column (from the left).

Then the following 6 lines describe the strings on each face of the cube. All of these strings are not empty and shorter than 12 characters (inclusive). In addition, they only consist of uppercase alphabets or digits. The faces where the strings are written are given as figure 1. Initially, the cube is placed on the start square in a direction as the face No. 1 is facing top and the upper direction of face No. 1 faces toward the top row of the map.

Figure 1. a net of a cube

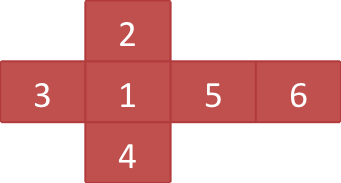
The last two lines contain two integers each that indicate the row number and column number of the start square and the goal square in this order. You can assume that the start square and the goal square are always different.

Output

Print the lexicographically minimal string in a line. If there is no path, print "no" in a line. If you can make the lexicographically minimal string infinitely longer, print "infinite" in a line.

Sample Input 1

1 3
+++
6
5
4
3
2
1
1 3
1 1

Output for the Sample Input 1

621

Sample Input 2

1 3
+++
1
2
3
4
5
6
1 3
1 1

Output for the Sample Input 2

infinite

Sample Input 3

1 3
...
1
2
3
4
5
6
1 3
1 1

Output for the Sample Input 3

no

Sample Input 4

3 3
->|
..v
.^<
JAG
2012
SUMMER
HOGE
HOGE
CAMP
1 1
2 2

Output for the Sample Input 4

JAGSUMMERCAMP2012JAGSUMMER2012

---