Problem D: Divide the Water
A scientist Arthur C. McDonell is conducting a very complex chemical experiment. This experiment requires a large number of very simple operations to pour water into every column of the vessel at the predetermined ratio. Tired of boring manual work, he was trying to automate the operation.
One day, he came upon the idea to use three-pronged tubes to divide the water flow. For example, when you want to pour water into two columns at the ratio of 1 : 1, you can use one three-pronged tube to split one source into two.
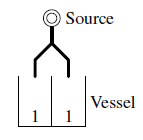
He wanted to apply this idea to split water from only one faucet to the experiment vessel at an arbitrary ratio, but it has gradually turned out to be impossible to set the configuration in general, due to the limitations coming from the following conditions:
- The vessel he is using has several columns aligned horizontally, and each column has its specific capacity. He cannot rearrange the order of the columns.
- There are enough number of glass tubes, rubber tubes and three-pronged tubes. A three-pronged tube always divides the water flow at the ratio of 1 : 1.
- Also there are enough number of fater faucets in his laboratory, but they are in the same height.
- A three-pronged tube cannot be used to combine two water flows. Moreover, each flow of water going out of the tubes must be poured into exactly one of the columns; he cannot discard water to the sewage, nor pour water into one column from two or more tubes.
- The water flows only downward. So he cannot place the tubes over the faucets, nor under the exit of another tubes. Moreover, the tubes cannot be crossed.
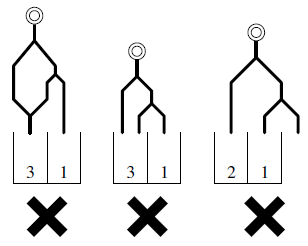
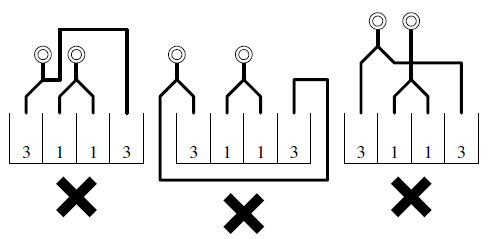
Still, Arthur did not want to give up. Although one-to-many division at an arbitrary ratio is impossible, he decided to minimize the number of faucets used. He asked you for a help to write a program to calculate the minimum number of faucets required to pour water into the vessel, for the number of columns and the ratio at which each column is going to be filled.
Input
The input consists of an integer sequence.
The first integer indicates N, the number of columns in the vessel. Then the following N integers describe the capacity by which each column should be filled. The i-th integer in this part specifies the ratio at which he is going to pour water into the i-th column.
You may assume that N ≤ 100, and for all i, vi ≤ 1000000.
Output
Output the number of the minimum faucet required to complete the operation.
Sample Input and Output
Input #1
2 1 1
Output #1
1
Input #2
2 3 1
Output #2
2
Input #3
2 2 1
Output #3
2
Input #4
4 3 1 1 3
Output #4
3
Input #5
3 1 2 1
Output #5
3
Input #6
5 1 2 3 4 5
Output #6
5
Input #7
7 8 8 1 1 2 4 8
Output #7
1