Problem F: Magnum Tornado

We have a toy that consists of a small racing circuit and a tiny car. For simplicity you can regard the circuit as a 2-dimensional closed loop, made of line segments and circular arcs. The circuit has no branchings. All segments and arcs are connected smoothly, i.e. there are no sharp corners.

The car travels on this circuit with one distinct feature: it is capable of jumping, which enables short cuts. It can jump at any time for any distance. The constraints are that 1) the traveling direction will never change during each jump, 2) the jumping direction needs to match the traveling direction at the time of take-off, and 3) the car must land on the circuit in parallel to the tangent at the landing point. Note that, however, the traveling direction at the landing point may be the opposite of the forward direction (we define forward direction as the direction from the starting point to the ending point of each line segment in the circuit.) That is, the car can traverse part of the circuit in the reverse direction.

Your job is to write a program which, given the shape of the circuit, calculates the per-lap length of the shortest route. You can ignore the height of the jump, i.e. just project the route onto the plane on which the circuit resides. The car must start from the starting point of the first line segment, heading towards the ending point of that segment, and must come back to the same starting point heading in the same direction.

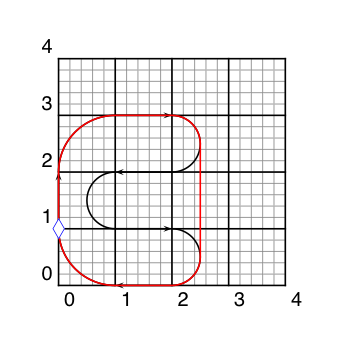
Figure 1 shows the solution for the first sample input.

Input

The input begins with a line that solely consists of an integer N (2 <= N <= 100), the number of line segments in the circuit. This is followed by N lines, where the i-th line corresponds to the i-th line segment (1 <= i <= N). Each of these N lines contains 4 integers x₀, y₀, x₁ and y₁ (-100 <= x₀, y₀, x₁, y₁ <= 100) in this order, separated by a space. Here (x₀, y₀) is the starting point and (x₁, y₁) is the ending point of the i-th line segment. For each i, the i-th and (i+1)-th line segments are connected smoothly by a circular arc, which you may assume exists uniquely (for simplicity, we consider the (N+1)-th line as the 1st line). You may also assume that, while two line segments or circular arcs may cross each other, they will never overlap nor be tangent to each other.

Output

For each test case, output one line that solely consists of a decimal value, representing the per-lap length. The output value should be in a decimal fraction and should not contain an error greater than 0.001.

Sample Input 1

5
0 1 0 2
1 3 2 3
2 2 1 2
1 1 2 1
2 0 1 0

Output for the Sample Input 1

9.712

Sample Input 2

12
4 5 4 6
3 7 1 7
0 8 0 10
1 11 3 11
4 10 4 9
5 8 99 8
100 7 100 4
99 3 4 3
3 2 3 1
2 0 1 0
0 1 0 3
1 4 3 4

Output for the Sample Input 2

27.406

---