G: Computer Onesan / コンピュータおねえさん
ある日,おねえさんは,子供たちに組合せの数え方について教えてあげることになりました.
そこで,おねえさんは,次のような問題を解いてみることにしました.
- 縦幅 1 ,横幅 1 の正方形を縦幅 N ,横幅 M の長方形に敷き詰めたときに,長方形の左上の頂点から右下の頂点への通り方が何通りあるかを数える
- 敷き詰めた正方形の辺の上しか通れない
- それぞれの通り方は,同じ場所を1度しか通らない
図1に,N = 2, M = 2 の場合の全ての通り方を示します. 図1では,全部で12通りの通り方を示しており,その経路は赤い太線で表しています.
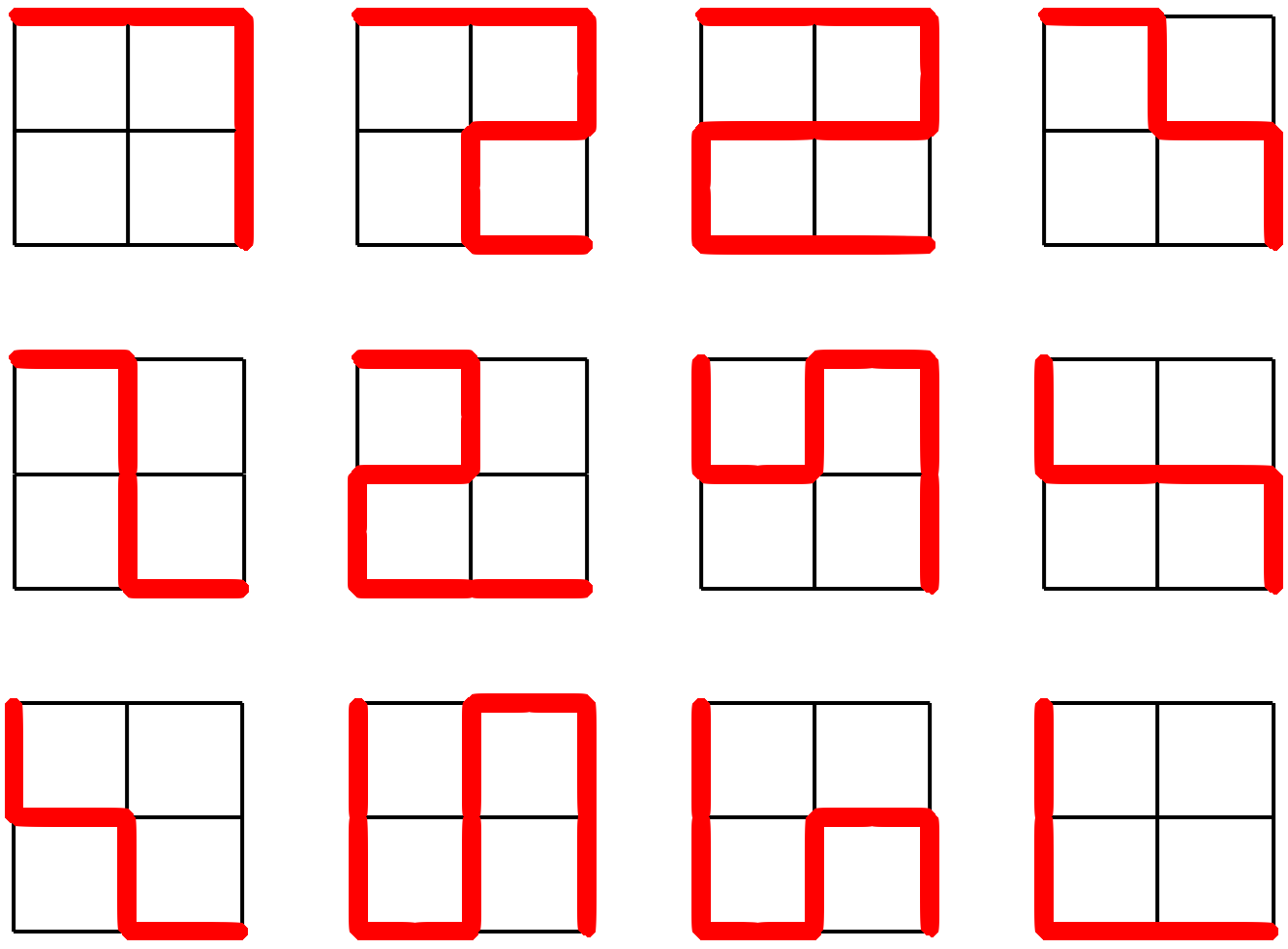
図1: N = 2, M = 2 の場合の全ての通り方
この問題では, N と M が少し大きくなるだけで,組合せの数が爆発的に増加してしまい,手で数えるのがとても難しくなってしまいます. そこで,おねえさんは,自分の頭脳をロボットに移植し,25万年をかけて,10 x 10 の場合の組合せの数を数える計画を立てました.
「10 x 10 なんて計算するとおねえさん死んじゃう!やめて!」
止める子供たちをよそに,おねえさんは,計算を開始します. おねえさんは,そこまでしてでも,子供たちに組合せ爆発のすごさを教えてあげたいのです.
おねえさんの熱意に心打たれたプログラマーのあなたは,この問題を解くプログラムを書いてあげることにしました. といっても,いきなり 10 x 10 を計算するプログラムを作るのは難しいので,手始めに M が小さい場合のプログラムを書くことにしました.
Input
入力は,1行に, N と M が半角スペースで与えられます. N は長方形の縦の幅で,1 <= N <= 100を満たします. M は長方形の横の幅で,1 <= M <= 2を満たします.
Output
入力に対する通り方の数を1行に出力してください. ただし,答えが非常に大きくなる場合があるので,1,000,000で割った余りを出力してください.
Sample Input 1
1 1
Sample Output 1
2
Sample Input 2
1 2
Sample Output 2
4
Sample Input 3
2 1
Sample Output 3
4
Sample Input 4
2 2
Sample Output 4
12
Sample Input 5
3 2
Sample Output 5
38