テトラ姫のパズル
パレス王国のテトラ姫は無類のパズル好きとして知られており,最近は自身が考案した「テトラパズル」に熱中している.
これは,正三角形のマスを敷き詰めたボードと,テトラブロックと呼ばれる 4 枚の正三角形のパネルからなる正四面体のブロックを使ったパズルである.
パズルの目的は,ボード上のすべてのテトラブロックを以下の条件をみたすように展開することである.
- 展開されたテトラブロックが,置かれていたマスおよび,それぞれに指定された異なる 2 つのマスを覆っている
- どのマスも,2 つ以上のパネルで覆われていない
図F-1はテトラパズルの問題例および,その解答例である.
★のマスと●のマスにテトラブロックが置かれており,それぞれが☆のマスと○のマスを覆うように指定されている.
解答例において,横線が引かれたマスは★のマスに置かれていたテトラブロックを展開して覆ったマス,縦線のマスは●のマスに置かれたテトラブロックで覆ったマスである.
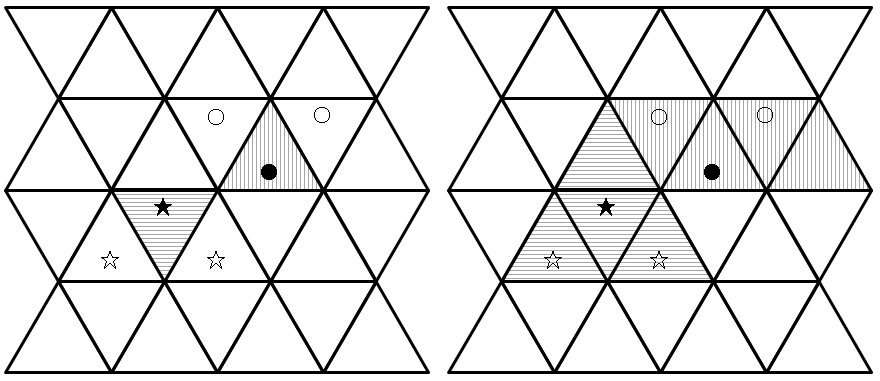
図 F-1: テトラパズルの問題例(左)および解答例(右)
図F-2は,上図の問題例における無効な解答例である. 左の例では★のマスの真上のマスが2つのパネルで覆われており,右の例ではそれぞれがテトラブロックを展開して得られる形状でないため,答えとしては認められない.
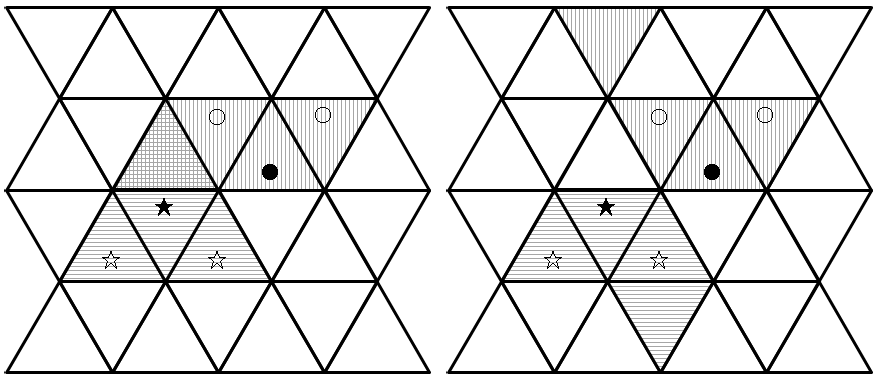
図 F-2: 無効な解答例
テトラ姫はパズルの面白さを多くの人に知ってもらうべく,来たる夏の祭典に向けてパズルの問題集を作った.
そして,王国で二番目のパズル好きとして姫から信頼を置かれているあなたは,問題集のチェック担当に任命された.
さて,チェック作業を進めていたあなたは困った事に気が付いた. 問題集には解が存在しないパズルが含まれているようなのだ. なるべく姫の作ったパズルを尊重したいと考えたあなたは,解が存在しないパズルについて,どれか 1 個のテトラブロックをそのテトラブロックが覆うべきマスの情報ごと削除することで,パズルを解けるものに変えることにした. 姫から言い渡されたチェックの締切りまではあと3時間しかない. 問題集を見なおして,手早く修正を済ませてしまおう.
Input
入力は複数のデータセットから構成される.
各データセットの形式は次の通りである.
n x1a y1a x1b y1b x1c y1c x2a y2a x2b y2b x2c y2c ... xna yna xnb ynb xnc ync
n (2 ≤ n ≤ 5,000) はボードに置かれたテトラブロックの数を表す整数である.
各テトラブロックには 1 から n の番号が割り当てられている.
続く n 行は,それぞれ 1 個のスペースで区切られた 6 個の整数からなる.
(xia, yia) は i 番目のテトラブロックが置かれているマスの座標を表し,(xib, yib) および,(xic, yic) は,それぞれ i 番目のテトラブロックを展開した時に覆うべきマスの座標を表す.
与えられる x 座標および y 座標の絶対値は 20,000 以下と仮定して良い.
また,与えられる座標は全て互いに異なると仮定して良い.
すなわち,同じマスに 2 個以上のテトラブロックが置かれる事や,テトラブロックが置かれているマスが覆うべきマスとして指定される事や,覆うべきマスが重複して指定される事はない.
各マスには図F-3のように座標が割り当てられている.
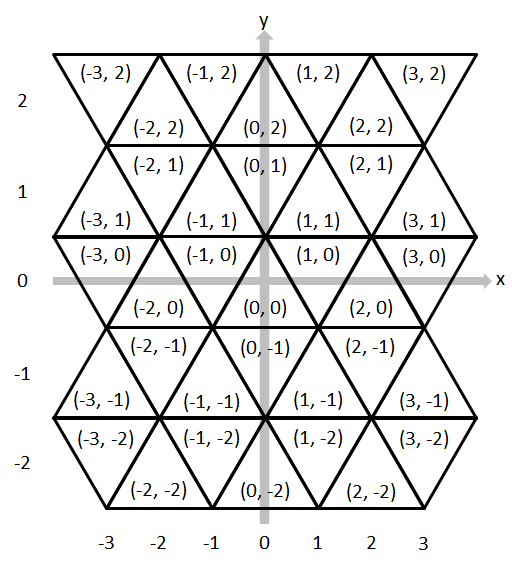
図 F-3: マスに割り当てられた座標
n=0 は入力の終わりを示す.これはデータセットには含めない.
Output
各データセットについて,テトラブロックを除くことなくパズルが解ける場合は Valid をそれぞれ 1 行に出力しなさい. テトラブロックを 1 個だけ除くことでパズルが解けるようになる場合は Remove を 1 行に出力し,続けて除くことでパズルが解けるようになるテトラブロックの番号を小さいものから順にそれぞれ 1 行に出力しなさい. 2 個以上のテトラブロックを除かないとパズルが解けるようにならない場合は Invalid を1行に出力しなさい.
Sample Input
3 2 3 2 2 2 1 2 0 1 -1 2 -1 -2 -1 -1 -1 -2 0 6 -1 0 1 0 0 -1 -2 -1 -3 -2 -4 -2 2 -1 2 0 1 -1 4 -2 3 -2 3 -1 1 1 0 1 -1 1 -3 -1 -1 -1 -2 0 5 -1 2 0 2 1 2 -3 1 -2 1 -2 2 -2 0 -2 -1 -3 0 1 -1 0 -1 -1 -1 1 0 2 0 2 -1 4 -2 0 -2 -1 -3 -1 -1 -1 0 -1 1 -1 2 -1 2 0 3 -1 -1 0 0 0 1 0 5 -2 1 3 -1 2 1 -5 2 -5 3 -4 2 -2 -1 0 -1 -3 -1 4 2 5 2 5 3 1 -1 2 -1 -1 -1 0
以下の図はそれぞれサンプルの配置を示している.
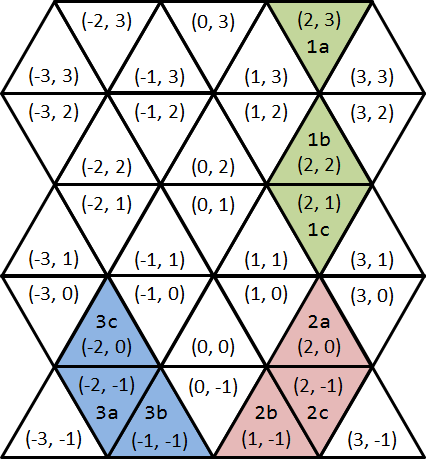
図 F-4: 1番目のサンプル
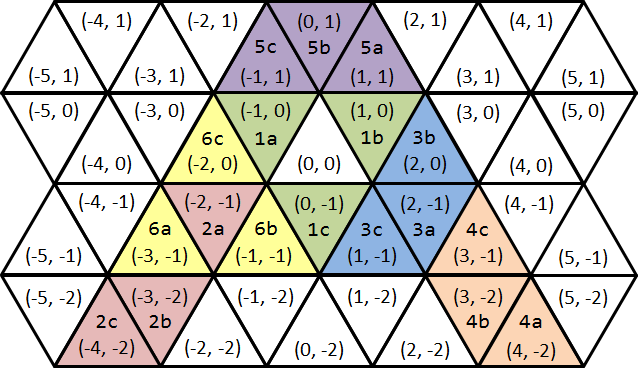
図 F-5: 2番目のサンプル

図 F-6: 3番目のサンプル
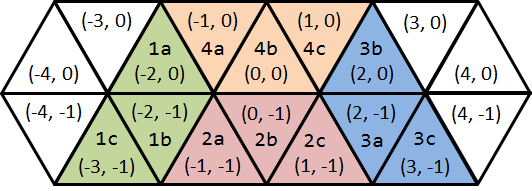
図 F-7: 4番目のサンプル
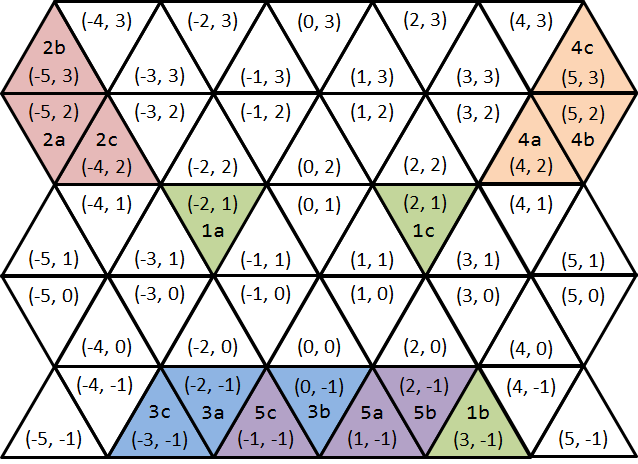
図 F-8: 5番目のサンプル
Output for Sample Input
Remove 1 Remove 2 6 Valid Remove 1 2 3 4 Invalid