鏡の迷路
誇り高き勇者であるあなたは、ついに魔王の元へ辿り着こうとしていた。しかし、魔王がいる玉座の間に辿り着くためには、魔王が用意した最終マップをクリアしなければならない。
このマップにおいては、全てのものが、上空から見た二次元平面図のように変化してしまう。人間は、このマップにおいては、ただの点に変形してしまう。マップは、1本の直線によって、2つの区域に区切られている。そして、ある一方の区域に人がいるとき、もう一方の区域の、直線に対して線対称となる位置に、人の鏡像が映し出される。
2つの区域それぞれには、複数の建物が存在する。建物と言っても、このマップでは、いくつかの点を繋いで出来上がる多角形であり、辺で囲まれた内側、および辺上が建物の内部となる。建物は、人とは違い、別の区域に鏡像を作り出すことはない。
あなたがこのマップに侵入すると、魔王の魔法により、いずれかの建物の内部に拘束される。あなたは、拘束されている建物の内部に1つだけ存在する脱出点に移動することでしか、マップをクリアすることはできない。さらに、あなたは、魔王に呪いをかけられ、自身の動きを制限されている。その制限とは、あなたのいる位置、およびあなたの鏡像の位置が、いずれかの建物内部に存在しなければならないというものである。この制限さえ守れば、あなたは自由に建物内部を移動することができる。
さて、あなたは、一刻も早くこのマップをクリアし、世界を滅ぼさんとする魔王を打ち倒さなければならない。あなたの初期位置が与えられたとき、脱出点へ移動するための最短路の距離を求めよ。ただし、脱出点へ移動できない場合は、永遠マップから脱出することができず、朽ち果てていくのみである。
Input
入力は複数のデータセットから構成される。 各データセットの形式は次の通りである。
N BUILDING1 ... BUILDINGN SX SY GX GY LX1 LY1 LX2 LY2
入力は、全て整数値である。 また、座標情報は、全て -10,000 <= x, y <= 10,000 であると仮定してよい。
N(1 <= N <= 100)は、建物の数である。その次に、N個の建物の情報が入力される。 BUILDINGiは、次の形式で入力される多角形である。
M X1 Y1 ... XM YM
M(3 <= M <= 50)は、多角形の頂点数を表す。 続いてM個の頂点、(Xi, Yi)が反時計回りで入力される。 (Xi, Yi)と(Xi+1, Yi+1)の頂点を繋いだ線分が多角形の一辺である。 ただし、M番目の頂点とは、1番目の頂点が繋がる。 多角形の連続する3つの頂点は、一直線上に並ばないものと仮定してよい。 また、多角形の各辺は、隣り合う辺以外とは、接触・交差することはないように入力される。 各多角形は、他の多角形に、接触・交差・内包することはない。
建物の情報が入力された後、始点(SX, SY)、脱出点(GX, GY)の情報が入力される。 始点と脱出点は、共に同じ建物の内部に存在する。 ただし、始点と脱出点の鏡像は、必ずしも建物の内部に存在するとは限らないため注意してほしい。 この場合は、もちろんマップをクリアすることはできない。 始点と脱出点は、必ず異なる位置に存在する。
最後に、直線の情報が入力される。 直線は、直線上に存在する2つの点(LX1, LY1)と(LX2, LY2)により表される。 この2つの点は、必ず異なる位置に存在する。 直線は、いずれの建物とも、接触・交差しないものと仮定してよい。
入力の終わりは、0が1つだけの行で与えられる。
Output
各データセットごとに、始点から脱出点までの最短距離を出力せよ。 解答の誤差は 0.00000001 (10-8) を超えてはならない。 精度に関する条件を満たしていれば、小数点以下は何桁数字を出力しても構わない。
脱出点まで辿り着けない場合は、"impossible"と出力せよ。
Sample Input
2 3 1 1 2 2 1 2 3 -1 1 -1 2 -2 2 1 1 2 2 0 0 0 1 2 10 1 1 7 1 7 5 5 5 5 3 6 3 6 2 3 2 3 5 1 5 10 -1 1 -1 5 -3 5 -3 3 -2 3 -2 2 -5 2 -5 5 -7 5 -7 1 2 4 6 4 0 0 0 1 2 7 -7 0 -5 0 -4 3 -3 0 -1 0 -1 4 -7 4 3 1 0 7 0 7 4 3 1 5 2 0 0 0 1 0
Output for Sample Input
1.4142135623730951 8.0 impossible
以下の図はそれぞれサンプルの配置を示している。 図G-1、G-2では、赤の経路が勇者自身の経路を示し、青の経路が勇者の鏡像の経路を示す。 図G-3では、始点から脱出点まで辿り着くことはできない。
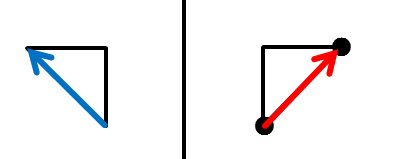
図G-1: 1番目のサンプル
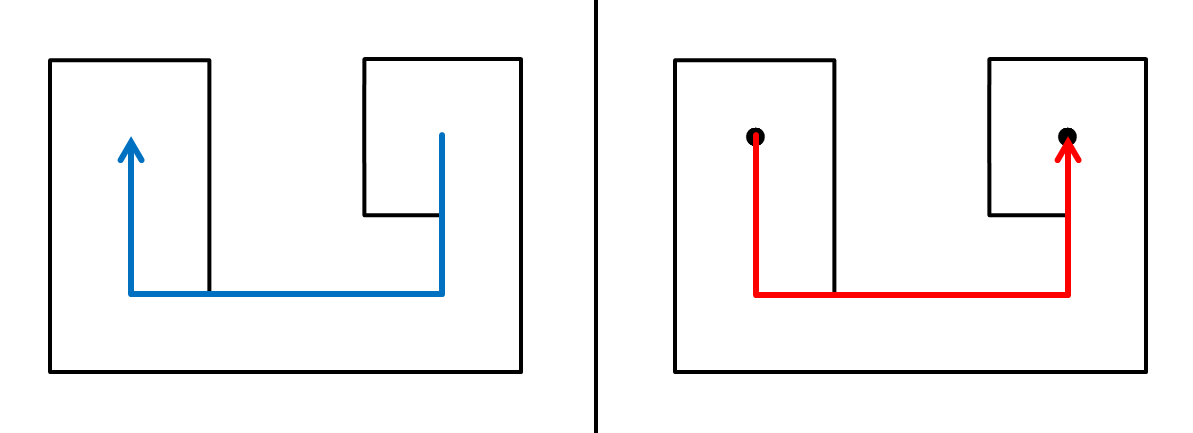
図G-2: 2番目のサンプル
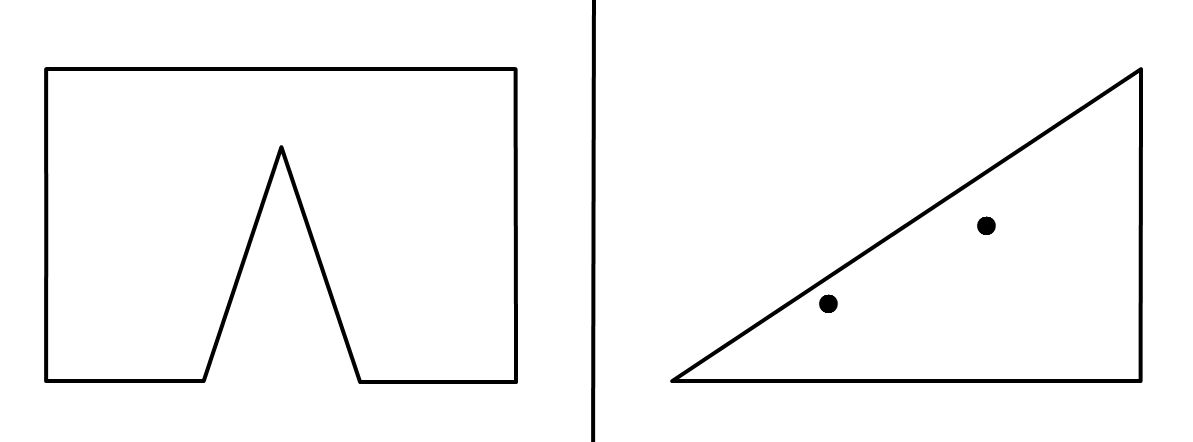
図G-3: 3番目のサンプル