Problem D: 2DはDecision Diagramの略
Problem Statement
BDD(Binary Decision Diagram)というデータ構造をご存知だろうか。近年、組み合わせ爆発お姉さんの動画関連でも話題になったZDDは、BDDが派生したデータ構造である。この問題は、BDDの基本的な実装を行うものである。
BDDとは、論理関数を表現する閉路のないグラフ(DAG)である。例えば、表1の真理値表を表わす論理関数は、図1のBDDとなる。BDDは、0エッジ(破線矢印)、1エッジ(実線矢印)、0終端ノード(0の四角)、1終端ノード(1の四角)、変数ノード(数字が書かれた丸)の5種類の部品からなる。0終端ノードと1終端ノードは、一番下にそれぞれ1つずつ存在する。各変数ノードからは、0エッジと1エッジ、それぞれが1つずつ出力されており、次のノードへとつながっている。各変数ノードは、ノードに書かれた番号の変数に対応しており、その変数の値が1ならば1エッジ側へ、0ならば0エッジ側へ辿る。そうして、一番上のノードから辿った結果、1終端ノードに行き着けば1が答え、0終端ノードに行き着けば0が答えとなる。例えば、表1の真理値表の「変数1=1, 変数2=0, 変数3=1」をBDDで辿ると、図1の太線のような辿り方となり、結果が1であることがわかる。この問題においては必ず、BDDの上側から1段ずつ、変数1、変数2、...、変数Nの順番に変数ノードが現れるものとする。
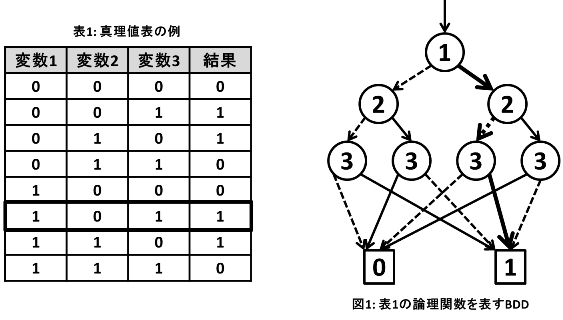
さて、この問題では、今説明した単純なBDDを、簡約化規則を利用して圧縮するプログラムを作成してもらう。簡約化規則とは、図2に示す2つの規則である。まず、図2(a)の規則は、変数ノードAがあったとき、「Aの0エッジの指す先=Aの1エッジの指す先」であるときに適用される。この場合、変数の値が0であろうと1であろうと遷移する先が1通りであるため、この変数ノードは必要のないものであるとわかる。そのため、この条件に当てはまる変数ノードは全て削除することができる。図2(b)の規則は、2つの変数ノードA, Bがあったとき、「Aの変数番号=Bの変数番号、かつAの0エッジの指す先=Bの0エッジの指す先、かつAの1エッジの指す先=Bの1エッジの指す先」であるときに適用される。この場合、二重に同じノードが存在していて無駄であることがわかるので、2つの変数ノードを1つの変数ノードとして共有することができる。
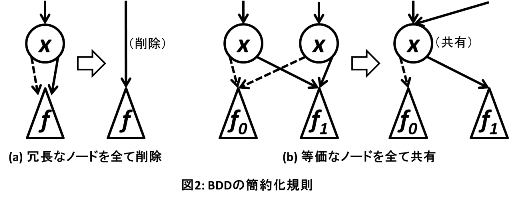
BDDの形が変わらなくなるまで簡約化規則を繰り返し用いると、図1のBDDは、図3(a)->(b)と変化していき、最終的に図3(c)のような、よりコンパクトなBDDへと変形する。もともと変数ノードが7個だったBDDが、変数ノード3個のBDDになったことがわかる。
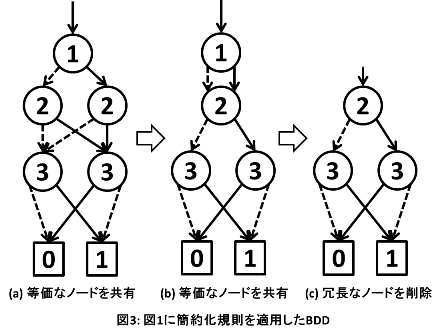
論理関数を表わす真理値表が入力されるので、簡約化規則を適用後のBDDの変数ノード数を出力せよ。
Input
各データセットは、以下の形式で入力される。N bit_line
Nは、論理関数の変数の数を表わす。bit_lineは真理値表を表わす、'1'と'0'からなる、2^Nの長さの文字列である。各文字は、
- 1文字目のビット: 変数1=0, 変数2=0, ..., 変数N-1=0, 変数N=0のときの結果
- 2文字目のビット: 変数1=0, 変数2=0, ..., 変数N-1=0, 変数N=1のときの結果
- 3文字目のビット: 変数1=0, 変数2=0, ..., 変数N-1=1, 変数N=0のときの結果
- 4文字目のビット: 変数1=0, 変数2=0, ..., 変数N-1=1, 変数N=1のときの結果
- ...
- 2^N文字目のビット:変数1=1, 変数2=1, ..., 変数N-1=1, 変数N=1のときの結果
Constraints
- 1 <= N <= 10
Output
簡約化規則適用後のBDDの変数ノード数を出力せよ。
Sample Input 1
3 01100110
Output for the Sample Input 1
3
Sample Input 2
2 0000
Output for the Sample Input 2
0
共有と削除を繰り返すと変数ノードはなくなる。
Sample Input 3
2 0110
Output for the Sample Input 3
3
簡約化規則を1回も適用することができない。
Sample Input 4
5 11110101011100110010111100010001
Output for the Sample Input 4
12