Problem E: Pie Chart is as easy as pie.

ICPC World Finals 3日目

この日、ティー氏はチーム内の言語使用割合を調べていた。 珍しいことに、我々のチームは使用言語を統一していない。 調査の結果、2人がC++、1人がJavaを使っていることが分かった。 さて、これをパイチャート（円グラフ）にしてみよう。

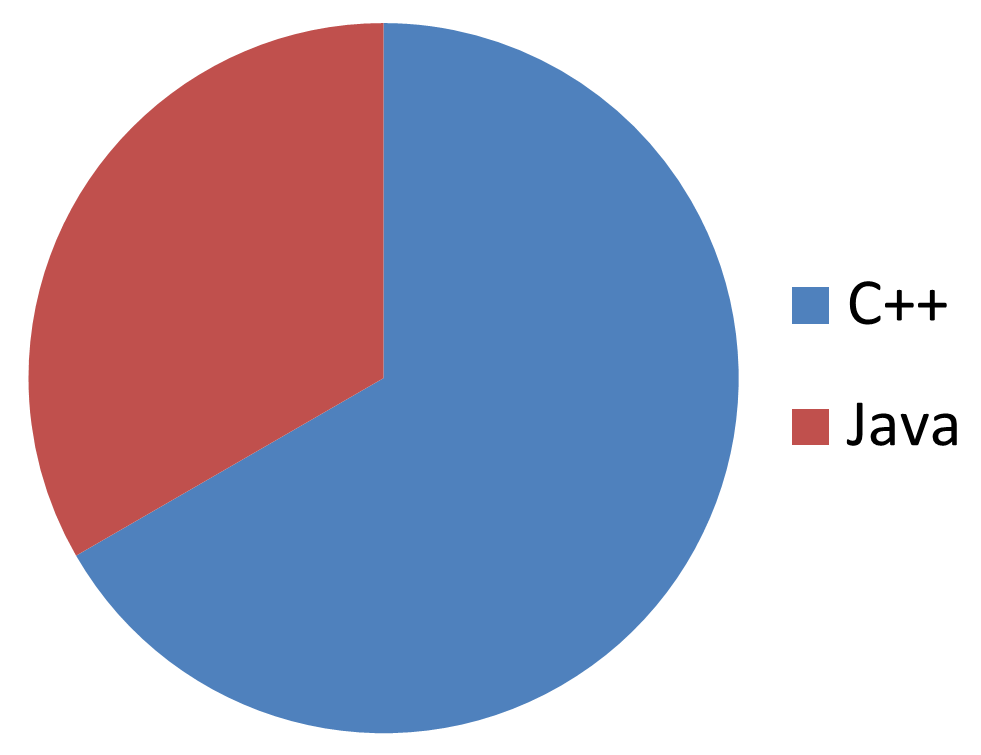
おや、Javaの使用割合が少ないように見えるな。 どう考えてもこんなはずはないので少々手を加えよう。 これは最近流行りのテクニックであり、 「パイチャートの中心座標をずらす」というものだ。 （皆さんはマネしてはいけません。）

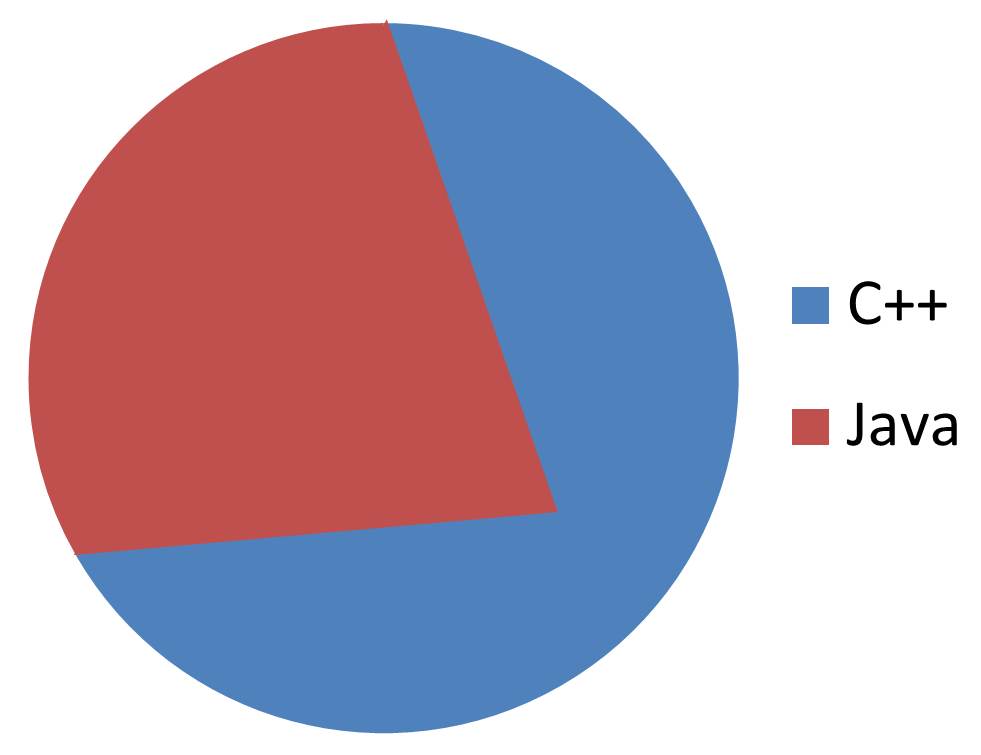
うむ、これでバランスがとれた。 ところで面積はどのように変わったのだろう？

問題

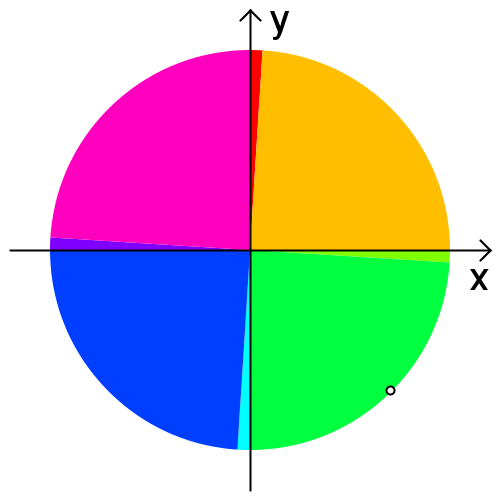
半径\(r\)、項目数\(n\)のパイチャート（円グラフ）が与えられる。 項目\(i\)の構成比率は\( p_{i} \)[%]であり、座標\( (0, r) \)から時計回りに項目が割り当てられる（下図を参照）。 パイチャートの中心座標が\( (0, 0) \)から\( (x, y) \)に変化した時、 各項目の占める面積は何%変化するかを求めよ。

入力

r x y n
p1 p2 … pn

1行目に パイチャートの半径\(r\)、中心のx座標\(x\)、y座標\(y\)、項目数\(n\)が空白区切りで与えられる。 2行目には、 項目\(i\)の構成比率\( p_{i} \)[%]が空白区切りで与えられる。

出力

1行目に各項目の占める面積の変化率[%]を「整数に切り捨てた値」を空白区切りで出力せよ。

制約

• 入力は全て整数で与えられる
• \( r = 100 \)
• \( x^{2} + y^{2} < r^{2} \)
• \( 2 \leq n \leq 10 \)
• \( p_{i} > 0 (1 \leq i \leq n) \)
• \( \sum_{1 \leq i \leq n}p_{i} = 100 \)
• \( (x, y) \)が高々距離\( 10^{-3} \)移動しても答えが変化しないことが保証される

入出力例

入力1

100 50 -50 2
67 33

出力1

71 156

項目1の面積は約21048から約15153に変化した。 変化率は15153/21048 ≒ 71.99%。

項目2の面積は約10367から約16262に変化した。 変化率は16262/10367 ≒ 156.86%。

入力2

100 -50 0 4
10 20 30 40

出力2

115 144 113 64

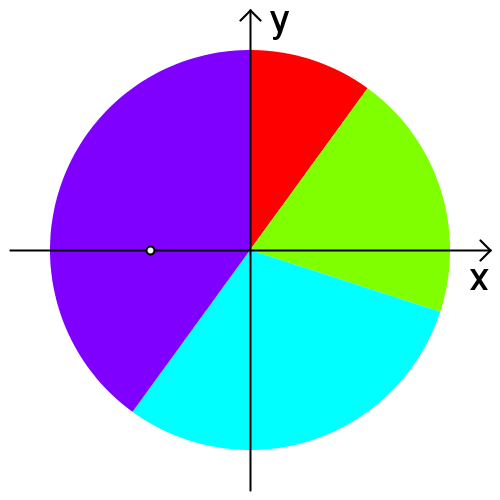
項目ごとのおよその面積の変化は以下の通り。

• 項目1: 3142 → 3619
• 項目2: 6283 → 9078
• 項目3: 9425 → 10675
• 項目4: 12566 → 8044

入力3

100 70 -70 8
1 24 1 24 1 24 1 24

出力3

167 97 27 10 32 102 172 189

---