Problem I: Reverse Game

あるところにオセロが趣味な女の子がいました。時間があるときに家族とオセロを楽しんでいます。

ある日、女の子はいつものようにオセロで遊ぼうとしました。ところが、みんな忙しくて誰も遊んでくれませんでした。 そこでオセロのボードとこまを使って１人で遊べるゲームを考え出しました。

問題

縦\( R \)マス、横\( C \)マスのマス目全てにオセロの駒が上面が黒あるいは白になるように配置されている。

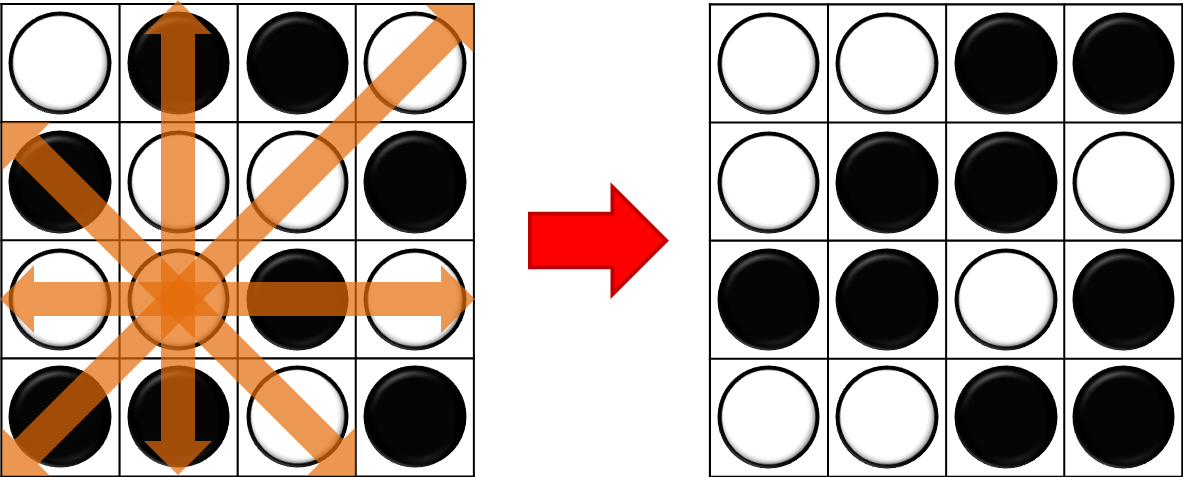
以下の図のように「あるマスを選んで、その上下左右斜め方向にある駒を全て裏返す」という操作を繰り返し行うことを考える。 全ての駒の上面を白にするような操作の仕方の個数を求めよ。 ただし、以下の条件を満たす必要がある。

• 同じマスに二度操作を行うことはできない
• 操作の順序は区別しない
• 全ての駒の上面が白になってから操作を続けることは可能である

入力

1行目に整数\( R \)と整数\( C \)がそれぞれ空白区切りで与えられる。

続けて\( R \)行に、それぞれ\( C \)個の整数値(0か1)が与えられる。\( r \)行目の\( c \)個目の整数は、マス目(r,c)の状態を表す。

1は上面が黒であることを、0は上面が白であることを表す。

出力

盤面の全ての駒の上面を白にすることができるなら、そのような操作の仕方の個数を\( 1000000009 (= 10 ^ 9 + 9) \)で割った余りを1行に出力せよ。

盤面の全ての駒の上面を白にすることができないなら、\( 0 \)と1行に出力せよ。

制約

• \(1 \leq R \leq 50, 1 \leq C \leq 50\)

サンプル入出力

入力1

1 3
1 1 1

出力1

4

\( \{(1,1)\}, \{(1,2)\}, \{(1,3)\}, \{(1,1),(1,2),(1,3)\} \)の4通りである。

入力2

1 3
1 0 1

出力2

0

入力3

2 4
0 1 0 1
1 0 1 0

出力3

1

---