C - Dowsing Machine / ダウジングマシーン
Story
世間ではXだとかYだとかで騒がしいけれど、これからの時代は"D"である。"パクリンモンスターD"は、秘密結社"R団"によって開発された"Dマシン"を使って"Dのひと"が財宝探索を行う大人気ゲームである。
このゲームでは、格子状マップのあるマスにいるDのひとが、隣接する上下左右のマスへの移動を繰り返し、財宝が存在するマスへの到達を目指す。 マップ上には財宝が存在するマスが1つだけある。 財宝が存在するマスは明らかにされていないため、Dマシンを使って存在する財宝のマスを絞り込んでから、財宝が存在するマスへ移動したい。
Dマシンを使うと、財宝が存在するマスを含む複数マスへの反応を示す。反応は、Dマシンを使ったときにDのひとが居たマスを基準に表現される。ただし、Dマシンは壊れていることがあり、Dマシンを使ったときに、財宝が存在し得ないマスへの反応を示すことがある。また、Dのひとが移動できない壁マスがマップ上に存在するため、財宝の存在するマスに移動できないこともある。DのひとはいろいろなマスでDマシンを使い、その反応を観測した。Dのひとは、財宝の存在するマスに到達できるだろうか。
Problem
高さ h 幅 w の二次元格子を考える。あるマス t_{i,j} は、次のいずれかの文字で表される。
- "." : 通行可能であることを表す。このマスには財宝が存在するかもしれない。
- "#" : 壁があり、通行不可能であることを表す。このマスには財宝は存在しない。
- "D" : 通行可能であり、Dのひとがいることを表す。このマスには財宝が存在するかもしれない。
Dのひとは、上下左右に隣接する通行可能なマスへ移動することができる。
Dマシンは使用した位置に応じて、図のような二次元格子内のいずれかのマス集合への反応を示す。下図の各矩形は,それぞれが半径 r_1, r_2, ..., r_d の正方形である。正方形の半径が r_k であるとは、正方形の一辺の長さが 2 r_k + 1 であることを意味する。
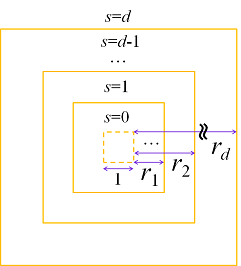
(x, y)でDマシンを使用したときに示された反応を s とする。1 \leq s \leq d-1のときは、(x, y)を中心とする半径 r_{s+1} の正方形から、 半径 r_s の正方形を除いた図形に含まれるマスに財宝が存在することを表す。s=0 のときは、(x, y)を中心とする半径 r_1 の正方形に含まれるマスに財宝が存在することを表す。s=d のときは、(x, y)を中心とする半径 r_d の正方形の外側のマスに財宝が存在することを表す。財宝が存在するマスは必ず1つだけ存在する。しかし、Dマシンが壊れている場合、Dマシンはこれに矛盾した反応を示す。
Dマシンの使用によって示された反応が複数与えられる。 Dマシンが確実に壊れている場合は"Broken"、Dのひとがいる位置から財宝の存在するマスに必ずたどり着ける場合は"Yes"、絶対にたどり着けない場合は"No"、たどり着けるかどうか分からない場合は"Unknown"を出力せよ。
Input
入力は以下の形式で与えらえる。
h w d n
t_{0,0}t_{0,1}...t_{0,w-1}
...
t_{h-1,0}t_{h-1,1}...t_{h-1,w-1}
r_1 r_2 ... r_d
x_1 y_1 s_1
...
x_n y_n s_n
1行目は4つの整数からなり,それぞれ,二次元格子の縦幅h、横幅w、 正方形の個数d、Dマシンを使用した回数nが空白1文字区切りで並んでいる。 続くh行では各マスの文字が与えられる。 i+2行目(0 \leq i < h)のj+1番目(0 \leq j < w)の文字t_{i,j}はマス(j,i)の文字を表す。 h+2行目では、各正方形の半径r_k(1 \leq k \leq d)が空白1文字区切りで与えられる。 続くn行では、Dマシンの反応が与えられる。 l+h+3行目(1 \leq l \leq n)では、x_l、y_l、s_lが空白1文字区切りで与えられ、マス(x_l, y_l)でDマシンを使用したときに反応s_lが示されたことを表す。
制約
- 1 \leq h \leq 50, 1 \leq w \leq 50, 1 \leq d \leq 10, 1 \leq n \leq 50
- t_{i,j}は"#", ".", "D"のいずれかであり、文字"D"は必ず1つだけ存在する
- 0 \leq r_k \leq 50であり,k > 1についてr_{k-1} < r_k
- 0 \leq x_l < w, 0 \leq y_l < h, 0 \leq s_l \leq d
- 文字"D"で表されるマスからの移動を繰り返すことで,マス(x_l, y_l)へ到達することができる
Output
"Broken", "Yes", "No", "Unknown"のいずれかのうち、適切なものを1行に出力せよ。行の最後では必ず改行を行うこと。
Sample Input 1
6 10 3 4 ########## #........# #...D....# #........# #........# ########## 2 4 6 3 2 0 7 4 2 8 4 3 1 4 1
Sample Output 1
Yes
Sample Input 2
6 10 2 3 ########## #.#......# ###......# #......D.# #........# ########## 1 2 3 2 1 3 1 1 1 3 1
Sample Output 2
No
Sample Input 3
6 10 3 1 ########## #........# #...D....# #........# #........# ########## 2 4 6 3 4 3
Sample Output 3
Broken
Sample Input 4
6 10 3 3 ########## #.#......# ###.D....# #.#......# #........# ########## 2 4 6 3 2 0 7 4 2 8 4 3
Sample Output 4
Unknown