E - Disappear Drive / 消えるドライヴ
Story
Dのひとはバスケットボールが好きだが、シュートが好きなため、他のテクニックはからっきしである。ドリブルは特に苦手で、相手の守備範囲に入ると必ずボールを奪われてしまう。そこでどんな相手も必ず抜き去る必殺のドリブルを編み出すことにした。努力の末、彼は遂に消えるドライヴ、"ディスアピアドライヴ"を完成させた。
ディスアピアドライヴは、相手を挑発することで集中力を奪い視線を外す"ディスディレクション"により隙を作り、その隙に次元(ディメンジョン)の壁を超えて相手の守備範囲をすり抜けてしまう完全無欠のドライヴである。しかし、次元の壁を超えることは体への負担が大きいため、次元を超えられる回数には制限がある。また、常に集中力を使うため、通常の移動を含め、方向転換が1度までしかできない。コート上でどのように動けば、ボールを奪われずに最短でゴールまで辿り着けるだろうか。
Problem
二次元平面上に、(0,0)を左下、(50,94)を右上とする長方形を考える。また、この平面上にはN個の円が存在し、i番目の円の中心の位置は(x_i,y_i)、半径はr_iである。円同士に重なりはない。
(25,0)を点S、(25,94)を点Gとし、SからGへ至る経路を考える。「経路」とは、(1)SとGを結んだ線分であるか、(2)長方形内部の任意の点Pについて線分SPと線分GPを結合したものからなる。SからGへと向かう経路の途中、一度ある円の内部に入ってからその円の内部から出るまでの間を「円の内部を通過する区間」と定義する。ただし、長方形・円の周上はそれぞれ長方形・円の内部には含まれないとする。
円の内部を通過する区間の数がD個以下であるような経路のうち、最短の経路の長さを求めよ。どうしてもゴールできないときは-1を返すこと。
Input
入力は以下の形式からなる。
N D x_1 y_1 r_1 ... x_N y_N r_N
1行目は2つの整数からなり、円の個数N、円の内部を通過できる回数Dが空白1文字区切りで与えられる。 続くN行は円の情報が与えられる。 i+1行目(1 \leq i \leq N)は3つの整数からなり、i番目の円の中心のx座標x_i、y座標y_i、半径r_iが空白1文字区切りで与えられる。
制約:
- 0 \leq N \leq 5
- 0 \leq D \leq 5
- 0 \leq x_i \leq 50
- 0 \leq y_i \leq 94
- 1 \leq r_i \leq 100
- 任意の2円間は10^{-5}以上離れていると仮定してよい。
- S,Gはそれぞれ任意の円の内部には含まれないと仮定してよい。
- S,Gはそれぞれ任意の円と10^{-5}以上離れていると仮定してよい。
- 最短経路における点Pは、長方形の周および任意の円周から10^{-5}以上離れていると仮定してよい。
Output
最短経路の長さを1行に出力せよ。行の最後では必ず改行を行うこと。 ただし、どうしてもゴールできないときは-1を返すこと。 正答に対し、10^{-7}以下の絶対誤差、あるいは相対誤差は許容される。
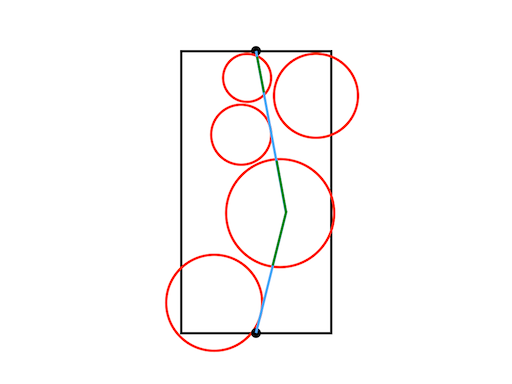
Sample Input 1
1 0 25 47 10
Sample Output 1
96.2027355887
消えることができないので、迂回した経路が最短である。
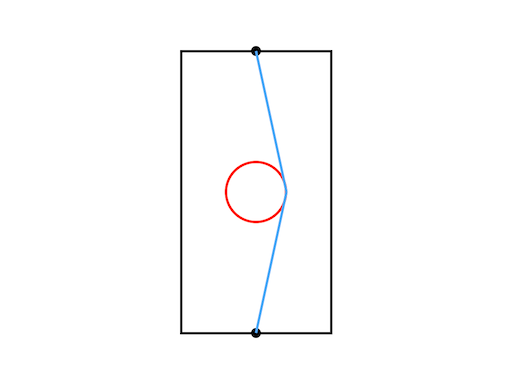
Sample Input 2
1 1 25 47 10
Sample Output 2
94.0000000000
消えることができるので、一直線に突き抜ければよい。
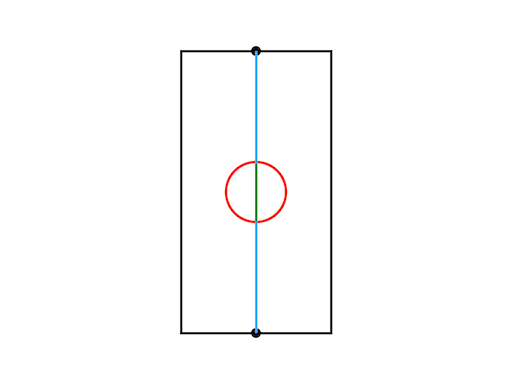
Sample Input 3
1 0 20 47 5
Sample Output 3
94.0000000000
円周上は円の内部に含まれないので、消えずに通過することができる。
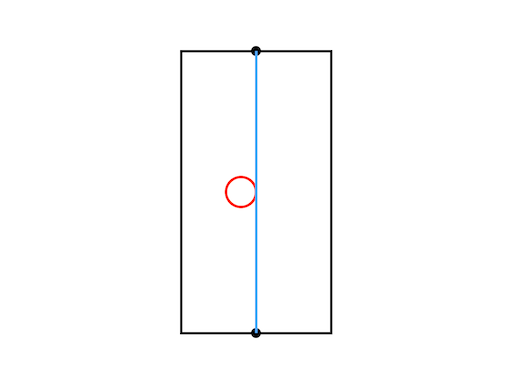
Sample Input 4
1 0 25 47 40
Sample Output 4
-1
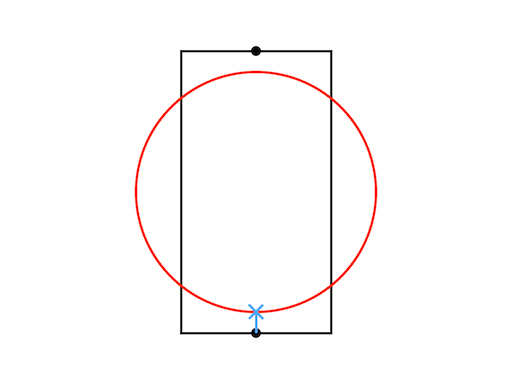
消えることも迂回することもできないため、ゴールに到達できない。
Sample Input 5
5 2 11 10 16 33 40 18 20 66 10 45 79 14 22 85 8
Sample Output 5
96.1320937224