F - Dangerous Delivery / 危険な輸送

Story

Dのひとは重大な使命を背負っていた。それはDAtaCoDer社長のDhokudai氏へ、次のDAtaCoDer Regular Contest(DARC)のD問題を届けることだ。Dのひとのアジトがある都市1からDAtaCoDer本社がある都市NまではN個の都市が一直線に並んでいる。この移動の間、不正を企む緑の三角形の集団がD問題を狙っており、その魔の手からD問題を守らねばならない。

幸い、Dのひとは次元(ディメンジョン)の壁を超えて移動する能力を持っているため、簡単に捕まるようなことはない。しかしこの移動法にはいくつかの欠点がある。第一に、移動を開始する際には隙ができてしまい、またその瞬間が見つかると、移動先までバレてしまう。緑の三角形達はそれぞれが複数の都市を見渡せるように監視し続けている。しかもDのひとの移動を読み、少しずつ都市Nの方向へ移動しているようだ。よって、多くの緑の三角形達に監視されている都市からの移動や、長い距離の移動は発見のリスクが高まってしまう。また第二の欠点として、次元の壁を超える移動は体への負担がかかるため、1日に1度しか使えない。次のDARCが開催されるD日後までに間に合わせるよう、ペース配分を考える必要もある。緑の三角形ごときにDのひとが捕捉されることなどまずありえないが、慎重派であるDのひとは、D日後までに都市1から都市Nに移動するためのリスクを最小化しようと考えた。

Problem

二次元平面上にN個の都市がある。都市1からNは左から右へ一直線上に並んでおり、都市iは位置(p_i,0)にある。p_i<p_{i+1} (1 \leq i < N)を満たす。

また、この二次元平面上にはM人の敵がおり、敵jは当初、位置(a_j,b_j)にいる。敵jは左方向について、上下45°の範囲を見張っている。すなわち、直線 y=x-a_j+b_j 以上で、かつ、直線y=-x+a_j+b_j 以下の領域に含まれる全ての都市が視界に入っている。また、すべての敵は1日ごとにちょうどXだけ右方向に移動する。すなわち、d日目の敵jの位置は(a_j+X(d-1),b_j)である。

ここで、d日目における都市iの監視度w_{d,i}は、d日目において都市iを視界に入れている敵の総数により定義される。このとき、d日目の都市iから都市kへの移動は、w_{d,i} \times |p_i-p_k|のリスクを負う。1日に1度しか移動できないとするとき、D日後までに都市1から都市Nまで移動する際のリスクの総和を最小化せよ。

Input

入力は以下の形式からなる。

N M D X
p_1 p_2 ... p_N
a_1 b_1
...
a_M b_M

1行目は4つの整数からなり、都市の数N、敵の数M、移動にかけてよい日数の上限D、1日ごとの敵の移動距離Xがそれぞれ空白1文字区切りで与えられる。 2行目はN個の整数からなり、i番目の整数は都市iの位置のx座標p_iが空白1文字区切りで与えられる。 続くM行は敵の位置情報が与えられる。 j+2行目(1 \leq j \leq M)は2つの整数からなり、敵jの1日目の位置のx座標a_j、y座標b_jが空白1文字区切りで与えられる。

制約:

• 1 \leq N \leq 10^4
• 1 \leq M \leq 10^4
• 1 \leq D \leq 10^2
• 1 \leq X \leq 10^6
• 0 \leq p_i, a_j \leq 10^6, -10^6 \leq b_j \leq 10^6
• p_i<p_{i+1}

Output

D日目までに都市Nにいるためのリスクの総和の最小値を1行に出力せよ。行の最後では必ず改行を行うこと。

Sample Input 1

3 2 2 1
0 3 6
1 1
3 -2

Sample Output 1

6

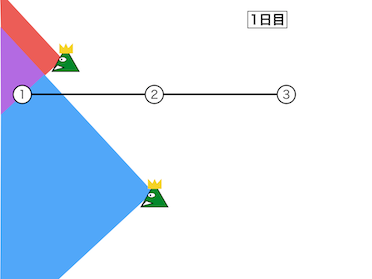
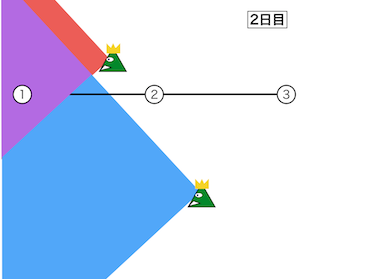
1日目、都市1は2人、都市2は0人、都市3は0人に監視されている。 2日目も同様に、都市1は2人、都市2は0人、都市3は0人に監視されている。 よって、1日目に都市1から都市2に移動してリスクが2 \times |3-0|=6、2日目に都市2から都市3へ移動してリスクが0 \times |6-3|=0の合計6が最小である。

Sample Input 2

3 2 2 1
0 3 6
2 1
3 -1

Sample Output 2

9

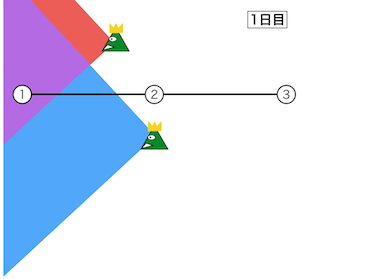
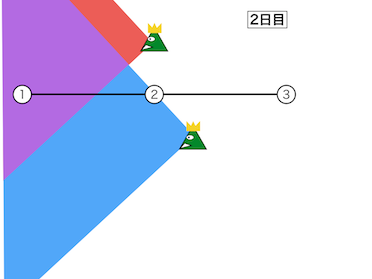
移動の仕方は1つ目のサンプルと同じだが、2日目は敵の移動により都市2の監視人数が1人増えるため、コストが1 \times |6-3|=3に変化する。 よって、最小リスクは9である。

Sample Input 3

10 8 5 3
0 8 10 13 17 20 21 29 30 45
18 2
50 -20
17 1
38 21
40 -11
0 0
0 0
22 -1

Sample Output 3

222

---