キョウトという街は古い寺社仏閣で有名な観光地である。

イクタ君は数人の友人とキョウト観光に来ていたが、全員が好き勝手に行動した結果、みんな迷子になってしまった。

そこでイクタ君は、なるべく早く全員と合流するためには集合場所をどこにするのがよいか考えることにした。

キョウトの道路は東西と南北に距離10の間隔で無数に走っており、無限に広がる正方格子とみなすことができる。

道路は直線であるとみなし、幅は無いものとする。 また、街の中心を基準として東に距離x、北に距離y移動した位置を(x,y)という座標で表す。

街の中心である(0,0)では東西の道路と南北の道路が交差している。

下図はキョウトの道路と、いくつかの点の座標を図示したものである。

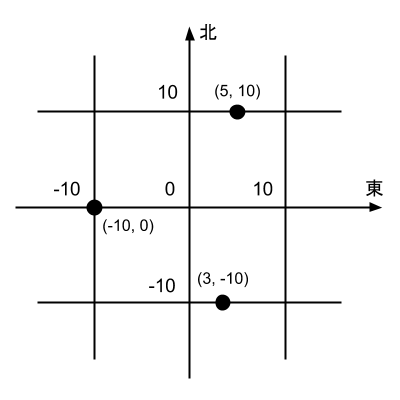
N人の観光客の座標(X_i,Y_i)が整数で与えられるので、N人が道路上を移動して1点に集合するのに必要な時間の最小値を答えよ。

観光客は時間1あたり距離1の速さで連続的に道路上を動くことができるとする。

与えられるN人の観光客の座標はそれぞれ相異なり、また全ての座標は道路上にあることが保証されている。

また、複数の観光客が同時に1点に存在したり、観光客同士がすれ違うように移動することも可能であるとする。

Input

入力は以下の形式で与えられる。

N
X₁ Y₁
...
X_N Y_N

1行目のNは観光客の人数である。 次のN行のうちi行目(1≤ i ≤ N)はi番目の観光客の位置(X_i, Y_i)を表している。 X_i,Y_iはそれぞれ整数で与えられる。

Constraints

入力中の各変数は以下の制約を満たす。

• 2 ≤ N ≤ 10000
• −10⁸ ≤ X_i, Y_i ≤ 10⁸
• i ≠ j のとき (X_i, Y_i) ≠ (X_j, Y_j)
• X_i と Y_i のうち少なくとも一方は10の倍数である

Output

問題の解を1行に出力せよ。 10⁻³までの絶対誤差を許容する。

Sample Input 1

3
5 10
-10 0
3 -10

Output for the Sample Input 1

14

• (0, 1)に集合すればよい（この入力例は問題文中の図と対応している）

Sample Input 2

2
0 0
0 1

Output for the Sample Input 2

0.5

• (0, 0.5)に集合すればよい（整数座標以外に集まる場合もあることに注意せよ）

Sample Input 3

4
100000000 100000000
100000000 -100000000
-100000000 100000000
-100000000 -100000000

Output for the Sample Input 3

200000000

---