Ayimok is a wizard.

His daily task is to arrange magical tiles in a line, and then cast a magic spell.

Magical tiles and their arrangement follow the rules below:

• Each magical tile has the shape of a trapezoid with a height of 1.
• Some magical tiles may overlap with other magical tiles.
• Magical tiles are arranged on the 2D coordinate system.
• Magical tiles' upper edge lay on a horizontal line, where its y coordinate is 1.
• Magical tiles' lower edge lay on a horizontal line, where its y coordinate is 0.

He has to remove these magical tiles away after he finishes casting a magic spell. One day, he found that removing a number of magical tiles is so tiresome, so he decided to simplify its process.

Now, he has learned "Magnetization Spell" to remove magical tiles efficiently. The spell removes a set of magical tiles at once. Any pair of two magical tiles in the set must overlap with each other.

For example, in Fig. 1, he can cast Magnetization Spell on all of three magical tiles to remove them away at once, since they all overlap with each other. (Note that the heights of magical tiles are intentionally changed for easier understandings.)

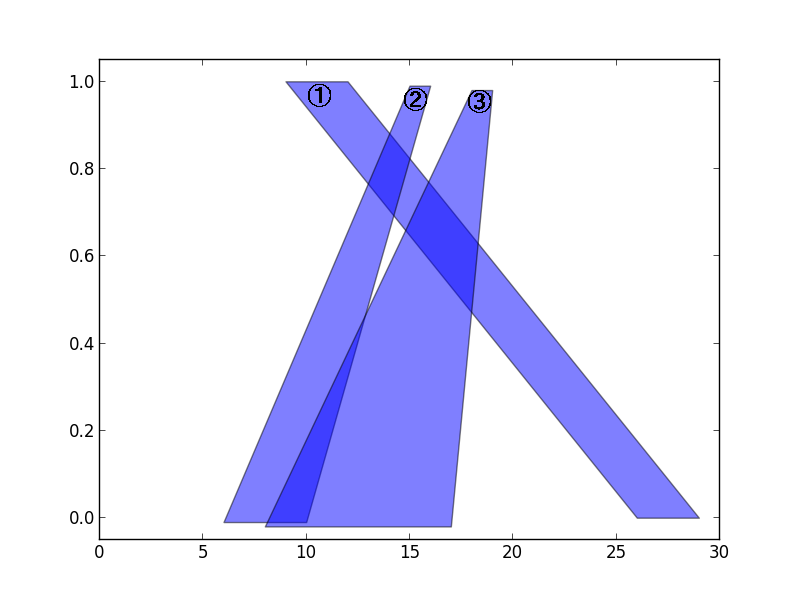
Fig. 1: Set of magical tiles which can be removed at once

However, in Fig. 2, he can not cast Magnetization Spell on all of three magical tiles at once, since tile 1 and tile 3 are not overlapped.

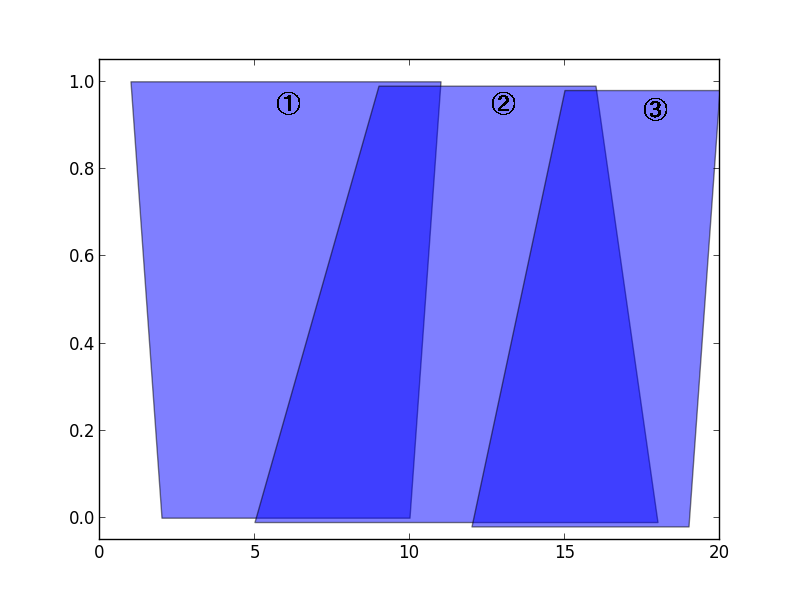
Fig. 2: Set of magical tiles which can NOT be removed at once

He wants to remove all the magical tiles with the minimum number of Magnetization Spells, because casting the spell requires magic power exhaustively.

Let's consider Fig. 3 case. He can remove all of magical tiles by casting Magnetization Spell three times; first spell for tile 1 and 2, second spell for tile 3 and 4, and third spell for tile 5 and 6.

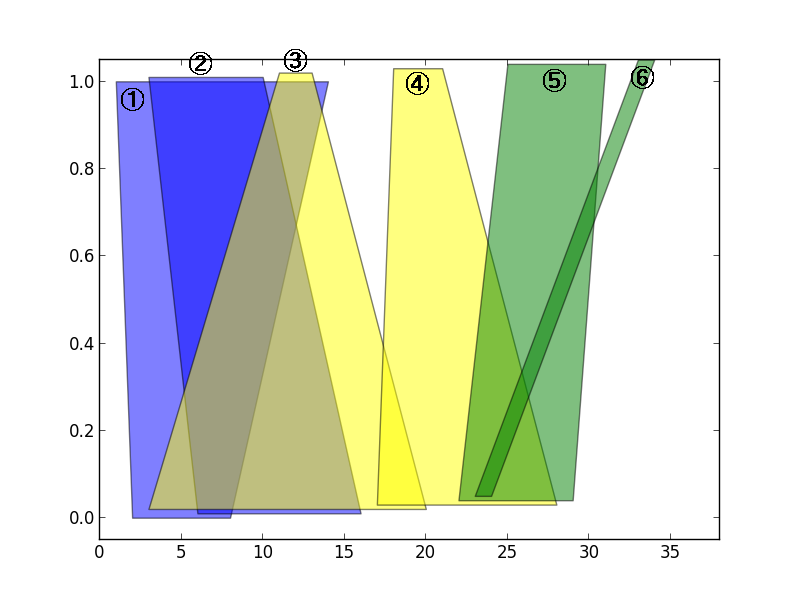
Fig. 3: One way to remove all magical tiles (NOT the minimum number of spells casted)

Actually, he can remove all of the magical tiles with casting Magnetization Spell just twice; first spell for tile 1, 2 and 3, second spell for tile 4, 5 and 6. And it is the minimum number of required spells for removing all magical tiles.

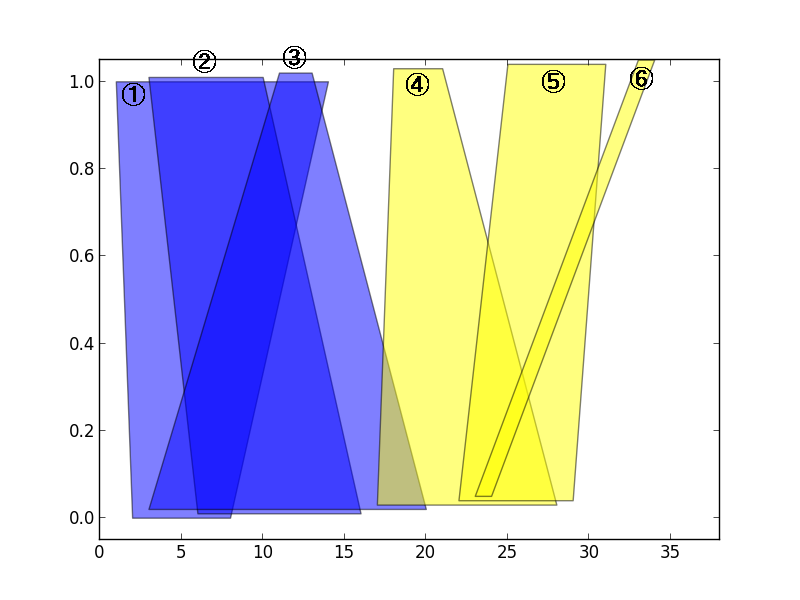
Fig. 4: The optimal way to remove all magical tiles(the minimum number of spells casted)

Given a set of magical tiles, your task is to create a program which outputs the minimum number of casting Magnetization Spell to remove all of these magical tiles away.

There might be a magical tile which does not overlap with other tiles, however, he still needs to cast Magnetization Spell to remove it.

Input

Input follows the following format:

N
xLower_{11} xLower_{12} xUpper_{11} xUpper_{12}
xLower_{21} xLower_{22} xUpper_{21} xUpper_{22}
xLower_{31} xLower_{32} xUpper_{31} xUpper_{32}
:
:
xLower_{N1} xLower_{N2} xUpper_{N1} xUpper_{N2}

The first line contains an integer N, which means the number of magical tiles.

Then, N lines which contain the information of magical tiles follow.

The (i+1)-th line includes four integers xLower_{i1}, xLower_{i2}, xUpper_{i1}, and xUpper_{i2}, which means i-th magical tile's corner points are located at (xLower_{i1}, 0), (xLower_{i2}, 0), (xUpper_{i1}, 1), (xUpper_{i2}, 1).

You can assume that no two magical tiles will share their corner points. That is, all xLower_{ij} are distinct, and all xUpper_{ij} are also distinct. The input follows the following constraints:

• 1 \leq N \leq 10^5
• 1 \leq xLower_{i1} < xLower_{i2} \leq 10^9
• 1 \leq xUpper_{i1} < xUpper_{i2} \leq 10^9
• All xLower_{ij} are distinct.
• All xUpper_{ij} are distinct.

Output

Your program must output the required minimum number of casting Magnetization Spell to remove all the magical tiles.

Sample Input 1

3
26 29 9 12
6 10 15 16
8 17 18 19

Output for the Sample Input 1

1

Sample Input 2

3
2 10 1 11
5 18 9 16
12 19 15 20

Output for the Sample Input 2

2

Sample Input 3

6
2 8 1 14
6 16 3 10
3 20 11 13
17 28 18 21
22 29 25 31
23 24 33 34

Output for the Sample Input 3

2

---