F : Todaiji / 東大寺
Problem
づいあ君は旅行が大好きである。奈良旅行に訪れたづいあ君は、東大寺にある柱の穴をくぐることにした。しかし、づいあ君は最近太りだしたため、穴に引っかかってしまうかもしれない。そこでづいあ君は、どこまで太っても大丈夫かを調べるプログラムを書くことにした。
簡単のため問題は平面上で考える。穴は2本の折れ線で、づいあ君は円で表すこととする。折れ線 1 は点 (0,0) が始点、点 (1000,0) が終点である。折れ線 2 は点 (0,1000) が始点、点 (1000,1000) が終点である。 づいあ君の全身が x < 0 の領域にある状態から、2 本の折れ線の間を通り、 x > 1000 の領域にづいあ君の全身が出た状態に到達できるような最大の直径を求めてほしい。通過する際の経路は自由であり、円が折れ線に接しても良い。
Input
入力は次のような形式で与えられる。
N1
x11 y11
x12 y12
...
x1N1 y1N1
N2
x21 y21
x22 y22
...
x2N2 y2N2
- N1 は1つ目の折れ線を構成する点の数である。
- x1i, y1i は、1つ目の折れ線を構成する i 番目の点の座標である。(x1i, y1i) と (x1(i+1), y1(i+1)) が結ばれる。
- (0,0) と (x11 , y11)、(x1N1 , y1N1) と (1000,0) がそれぞれ線で結ばれる。
- 2つ目の折れ線についても折れ線1と同様の形式で入力される。ただし、(x21 , y21) と結ばれるのは (0,1000)、(x2N2 , y2N2) と結ばれるのは (1000,1000) である。
Constraints
- 入力は全て整数である。
- 1 ≦ N1, N2 ≦ 50
- 0 ≦ xij , yij ≦ 1000
- xij ≦ xi(j+1)
- 折れ線は自分自身と交わらない。
- 2 本の折れ線は交わらない。
Output
2 本の折れ線の間を通過できる、づいあ君の体の最大の直径を1行で出力せよ。10-6 までの誤差は許される。
Samples
Sapmle Input 1
2 300 300 700 300 2 300 700 700 700
Sapmle Output 1
400.0000000000
Sapmle Input 2
31 53 334 96 201 99 129 114 365 123 39 186 257 195 247 233 335 256 79 302 217 404 302 411 222 428 422 433 388 441 443 468 309 497 408 518 218 537 361 538 193 541 447 580 16 606 185 610 178 737 421 754 210 805 418 849 416 876 262 878 220 948 207 28 7 919 89 640 145 656 152 963 204 558 252 630 269 690 325 629 357 583 454 593 523 648 538 949 541 821 559 655 581 614 593 877 607 571 631 817 682 942 776 529 810 606 813 598 834 778 838 999 910 661 920 824 982 517 987 689
Sapmle Output 2
114.7257599670
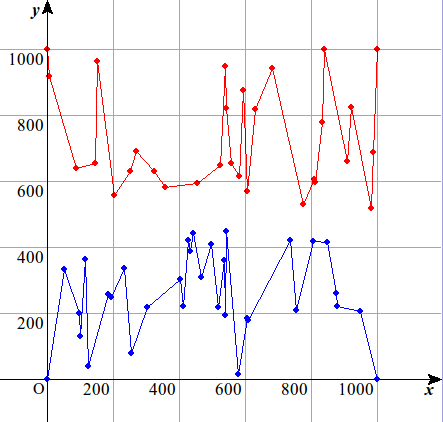
サンプル 2 を図示するとこのようになる。