Line Gimmick
You are in front of a linear gimmick of a game. It consists of $N$ panels in a row, and each of them displays a right or a left arrow.
You can step in this gimmick from any panel. Once you get on a panel, you are forced to move following the direction of the arrow shown on the panel and the panel will be removed immediately. You keep moving in the same direction until you get on another panel, and if you reach a panel, you turn in (or keep) the direction of the arrow on the panel. The panels you passed are also removed. You repeat this procedure, and when there is no panel in your current direction, you get out of the gimmick.
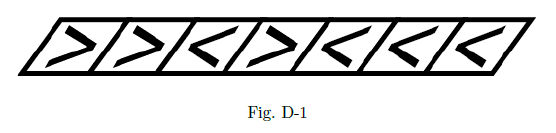
For example, when the gimmick is the following image and you first get on the 2nd panel from the left, your moves are as follows.
- Move right and remove the 2nd panel.
- Move left and remove the 3rd panel.
- Move right and remove the 1st panel.
- Move right and remove the 4th panel.
- Move left and remove the 5th panel.
- Get out of the gimmick.
You are given a gimmick with $N$ panels. Compute the maximum number of removed panels after you get out of the gimmick.
Input
The input consists of two lines. The first line contains an integer $N$ ($1 \leq N \leq 100,000$) which represents the number of the panels in the gimmick. The second line contains a character string $S$ of length $N$, which consists of '>' or '<'. The $i$-th character of $S$ corresponds to the direction of the arrow on the $i$-th panel from the left. '<' and '>' denote left and right directions respectively.
Output
Output the maximum number of removed panels after you get out of the gimmick.
Sample Input 1
7 >><><<<
Output for the Sample Input 1
7
Sample Input 2
5 >><<<
Output for the Sample Input 2
5
Sample Input 3
6 ><<><<
Output for the Sample Input 3
6
Sample Input 4
7 <<><<>>
Output for the Sample Input 4
5