D - インビジブル
Problem Statement
あなたは友達と"インビジブル"というカードゲームを遊ぼうとしている. このカードゲームでは,"得点カード"と"妨害カード"という2種類のカードを使う. それぞれの得点カードには,正の値が書かれている.このカードゲームのルールは次の通りである.
- ゲームはプレイヤー1とプレイヤー2の2人のプレイヤーで行われる.ゲームはプレイヤー1のターンから始まる.
- 場には,1つのスタックと2つのデッキがある.スタックは,2人のプレイヤーが置いたカードからなる.また,それぞれのプレイヤーが持つデッキはそのプレイヤーが持つ得点カードと妨害カードからなる.プレイヤーは自分,もしくは相手デッキのカードの順番をいつでも確認できる.ゲームの開始時点ではスタックには1枚もカードはない.
- 2人のプレイヤーは交互に次の2つの行動のどちらかをちょうど1回行う.
- 自分のデッキの一番上のカードをスタックの一番上に置く.ただし,この行動は自分のデッキにカードが1枚も存在しない時には行うことができない.
- 自分のターンをパスする.
- プレイヤーがターンをパスした時,次の処理を行う.
- 各プレイヤーは次の2つの条件を満たすスタック中のすべての得点カードを得る.得た得点カードは場から取り除かれる.
- 自分がスタックにおいた得点カードである.
- 相手が置いたどの妨害カードよりも上にある (スタック中に相手の妨害カードが存在しないとき,プレイヤーは自分がスタックに置いたすべてのカードを得る).
- スタックのカードをすべて取り除く.
- 各プレイヤーは次の2つの条件を満たすスタック中のすべての得点カードを得る.得た得点カードは場から取り除かれる.
もしスタックにカードがない状態で両プレイヤーが連続してパスした場合,ゲームを終了する. 各プレイヤーの最終的なスコアは,各プレイヤーが得た得点カードに書かれた数の総和である.
各プレイヤーは,自分のスコアから相手のスコアを引いた値を最大化するために最適な行動をとる. あなたの仕事は,与えられた各プレイヤーのデッキに対し,各プレイヤーが最適に行動したときのプレイヤー1のスコアとプレイヤー2のスコアの差を計算することである.
Input
入力は次のような形式の単一テストケースからなる.
$n$ $m$
$a_1$ $a_2$ $\dots$ $a_n$
$b_1$ $b_2$ $\dots$ $b_m$
1行目は山札の枚数を表す正の整数 $n$, $m$ ($1 \le n, m \le 50$) からなる. 2行目は $n$ 個の整数からなり,$a_i$ はプレイヤー1のデッキの上から $i$ 番目のカードを表す ($1 \le i \le n$).$a_i$ は $1$ 以上,$1{,}000{,}000$ 以下,または $-1$ である. 3行目は $m$ 個の整数からなり,$b_j$ はプレイヤー2のデッキの上から $j$ 番目のカードを表す ($1 \le j \le m$).$b_j$ は $1$ 以上,$1{,}000{,}000$ 以下,または $-1$ である. $a_i$, $b_j$ が正の整数の時は得点カードを表し,$-1$ の時は妨害カードを表す.
Output
お互いのプレイヤーが最適に行動した時の (プレイヤー1のスコア) - (プレイヤー2のスコア) を出力せよ.
Sample Input 1
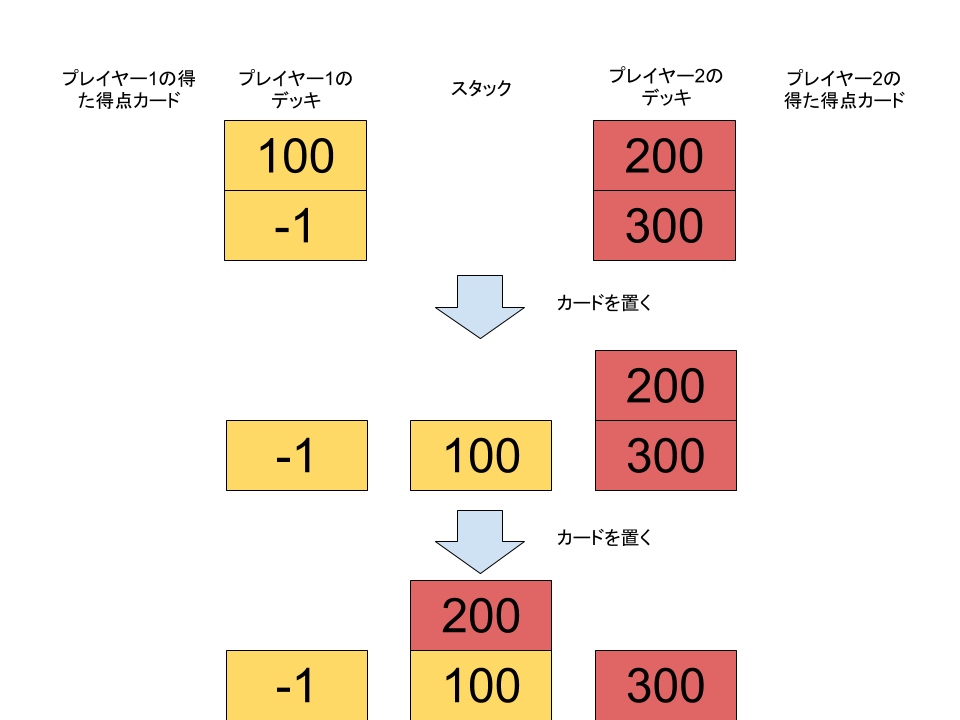
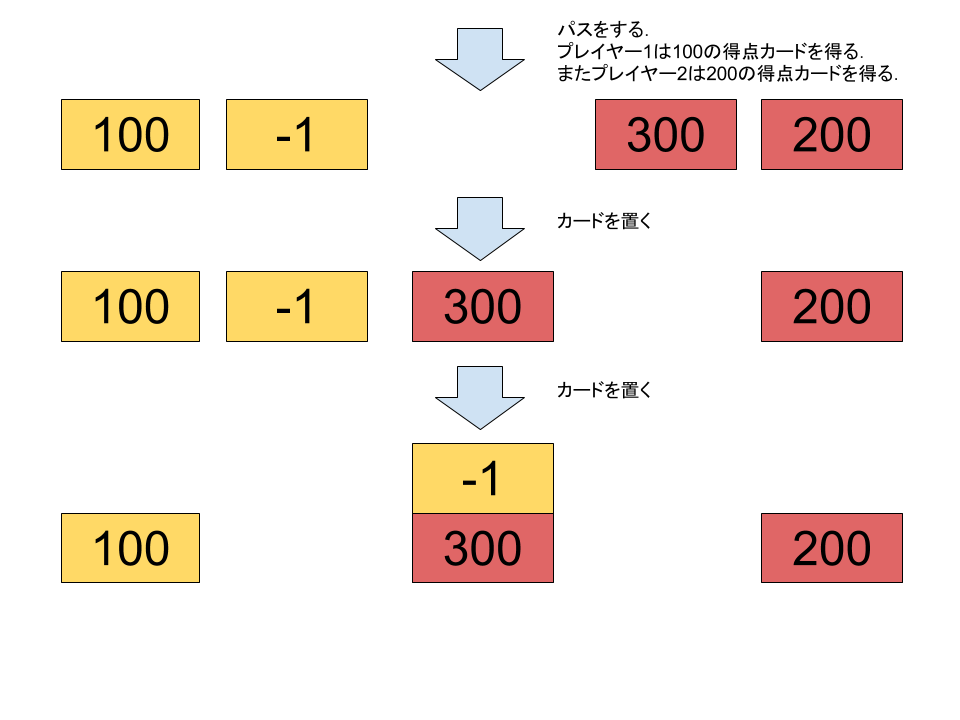
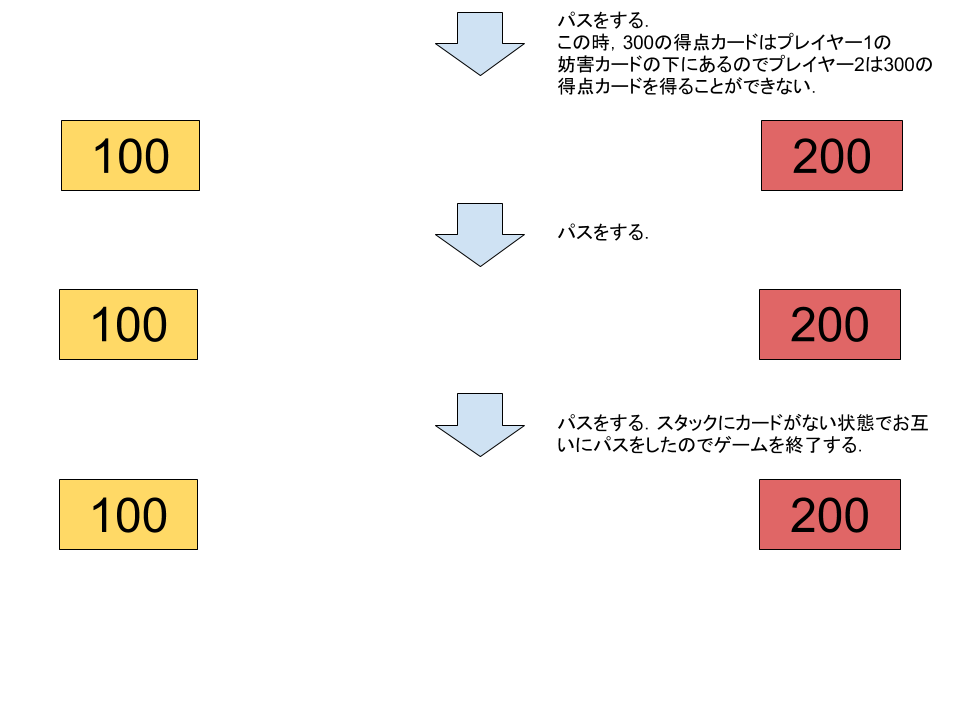
2 2 100 -1 200 300
Output for the Sample Input 1
-100
Sample Input 2
3 5 10 30 -1 -1 90 20 10 -1
Output for the Sample Input 2
0
Sample Input 3
4 5 15 20 10 30 50 30 10 20 25
Output for the Sample Input 3
-60