E - 選挙活動

Problem Statement

あなたは次回の選挙の候補者であるX氏の支援者である． X氏は駅前での街頭演説を予定しており，できるだけ多くの有権者に見てもらえる場所で演説しようと考えている．

駅前は $N$ 個の障害物と $M$ 人の有権者が存在している二次元平面として与えられる． 各障害物は多角形であらわされ，その多角形の内側の領域が障害物となる．多角形の辺上は障害物に含まれない． また，有権者は平面上の点としてあらわされる． ある有権者の位置とX氏の位置を結ぶ線分上に障害物が存在しないとき，その有権者はX氏を見ることができる．

あなたの仕事は，駅前の障害物と有権者の情報をもとに，もっとも多くの有権者に見てもらえる地点を探すことだ． 最大で何人の有権者から見えるように演説することができるかを求めよ．

Input

入力は以下のフォーマットで与えられる．

$N$ $M$
$polygon_1$
$polygon_2$
$...$
$polygon_N$
$x_1$ $y_1$
$x_2$ $y_2$
$...$
$x_M$ $y_M$

データセットの最初の行は空白文字1つで区切られた2個の整数 $N$, $M$ からなる． $N$ $(1 \le N \le 5)$ は駅前にある障害物の個数であり，$M$ $(1 \le M \le 10)$ は駅前にいる有権者の数である． 続く行から $N$ 個の障害物の情報が与えられる．1つの障害物を表す入力は以下の形式で与えられる．

$L$
$x_1$ $y_1$
$x_2$ $y_2$
$...$
$x_L$ $y_L$

各障害物情報の最初の行はその障害物をあらわす多角形に含まれる頂点の数 $L$ である． その後の $L$ 行には多角形の頂点の座標を表す整数の組が反時計回りに記されている．なお，障害物を構成する頂点数の合計は $15$ 個以下となる．

$N$ 個の障害物の情報の後に続く $M$ 行には有権者のいる座標を表す整数の組が与えられる．

また，各テストケースは以下の条件を満たす：

1. $ 0 \le |x_i|, |y_i| \le 20 $
2. 多角形の頂点または有権者のいる場所の座標はすべて互いに異なる．
3. 多角形の頂点または有権者のいる場所の座標のうち3点が同一直線状に存在することはない．
4. 2つの異なる多角形同士は交差を持たない．
5. 各多角形は自己交差を持たない．
6. 多角形の内部に有権者が存在することはない．

Output

最大で何人の有権者が演説を見られるようになるかを1行に出力せよ．

Sample Input 1

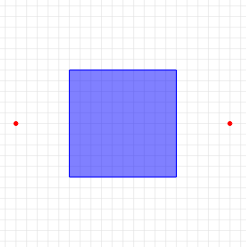
1 2
4
5 5
15 5
15 15
5 15
0 10
20 10

Output for the Sample Input 1

2

Sample Input 2

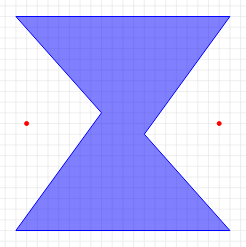
1 2
6
0 0
20 0
12 9
20 20
0 20
8 11
1 10
19 10

Output for the Sample Input 2

1

Sample Input 3

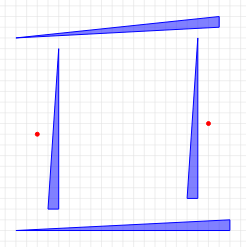
4 2
3
0 0
20 0
20 1
3
0 18
19 19
19 20
3
3 2
4 2
4 17
3
16 3
17 3
17 18
2 9
18 10

Output for the Sample Input 3

1

Sample Input 4

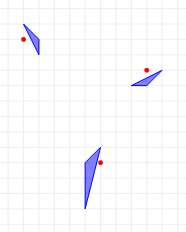
3 3
3
0 -2
-1 -3
-1 -6
3
2 2
3 2
4 3
3
-4 4
-4 5
-5 6
0 -3
3 3
-5 5

Output for the Sample Input 4

3

Sample Input 5

2 2
4
2 0
1 2
-1 2
-2 0
4
3 3
3 4
-3 4
-3 3
2 1
-2 1

Output for the Sample Input 5

2

Sample Input 6

1 1
4
1 1
-1 1
-1 -1
1 -1
0 2

Output for the Sample Input 6

1

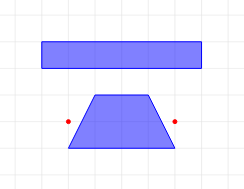
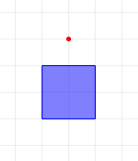
各入力例の障害物および有権者の配置は，それぞれ以下の図のようになっている．

---