G: 塗るだけ / Paint
問題文
情太くんと立子さんは, 平面の世界にある庭付きの家に住んでいる.二人は点とみなせ, 庭は $N$ 頂点の単純多角形 (隣り合わないどの $2$ 辺も交差も接触もしない多角形) の形をしている.
ある日,二人は一本の伸び縮みするローラーを手に入れた. ローラーは線分とみなせ,ローラーが通過した領域に色を塗ることができる. 二人はローラーを使って庭全体に色を塗りたいと思っている.
作業の前に,二人は以下のような準備を上から順に行う.
- 庭の内部の任意の $1$ 箇所に杭を打つ.
- 庭の外部のある $1$ 点に集まる.
- 十分に長い紐を用意し,片方の端を情太くん,もう一方の端を立子さんの体に結ぶ.
- 情太くんがローラーの片方の端を,立子さんがもう一方の端を持つ.
準備ができたら,以下のルールに従って塗り始める. ただし,ローラーは杭の上空を通過させることができるが,紐はできない.
- 庭のどの部分から塗り始めてもよい.
- 庭の外部または周上を移動できるが,内部に入ってはいけない.
- 塗り終わるまでローラーから手を離してはいけない.
さらに,塗り終わったときに以下の条件を満たしていなければならない.
- 二人が再びある $1$ 点に集まっている.
- 庭の内部の任意の点の上をローラーが通過している.
- 二人の体の紐を解き,両端を結んで輪を作る.この輪を外から引っ張ったときに,杭に引っかかって抜けない.
さて,二人はできるだけ離れたくないので,塗っている最中にとる二人の距離の最大値を最小化したい. 二人に代わってそのような値を求めてほしい.
入力
入力は以下の形式で与えられる.$N$ は多角形を構成する頂点の数, $(x_i,y_i)$ はある頂点から始めて時計回りまたは反時計回りに見たときの $i$ 番目の点の座標である.
$N$
$x_1 \ y_1$
$\vdots$
$x_N \ y_N$
制約
$3 \leq N \leq 50$
$|x_i|, |y_i| \leq 100$
全て整数である
頂点は時計回りまたは反時計回りに与えられる
庭の形は単純多角形である
周上の連続する $3$ 点は一直線上に存在しない
出力
答えを $1$ 行で出力せよ.$10^{-5}$ 未満の絶対誤差は許容される.
サンプル
各サンプルでの庭の形と塗り終わるまでのローラーの動きを図示すると以下のようになる.整数は時刻を表す.図示する都合上ローラーの動きは飛び飛びに示したが,実際には連続的に動いている. ローラーが太くなっている部分で距離の最大値を達成している.
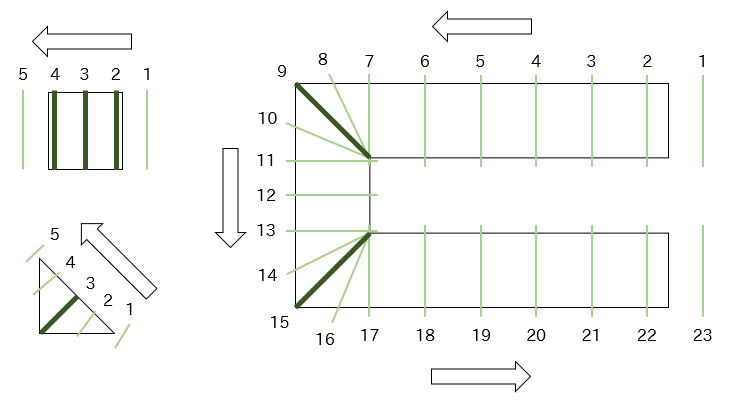
サンプル入力1
4 0 0 0 1 1 1 1 0
サンプル出力1
1
サンプル入力2
3 0 0 0 1 1 0
サンプル出力2
0.7071067811865476
サンプル入力3
8 0 0 5 0 5 3 0 3 0 2 4 2 4 1 0 1
サンプル出力3
1.4142135623730951