Problem Statement

"Rooks Game" is a single-player game and uses a chessboard which has $N \times N$ grid and $M$ rook pieces.

A rook moves through any number of unoccupied squares horizontally or vertically. When a rook can attack another rook, it can capture the rook and move to the square which was occupied. Note that, in Rooks Game, we don't distinguish between white and black, in other words, every rook can capture any of other rooks.

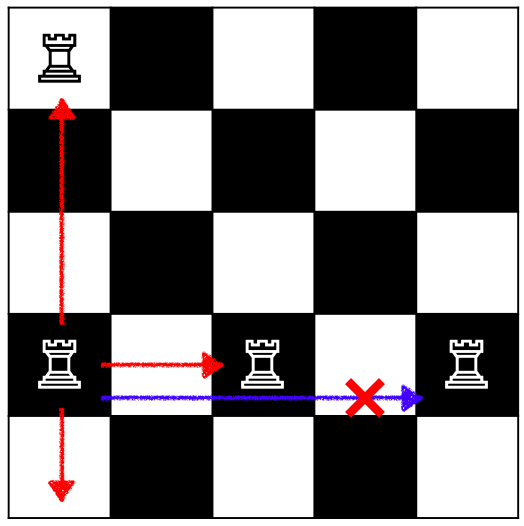
Initially, there are $M$ rooks on the board. In each move, a rook captures another rook. The player repeats captures until any rook cannot be captured. There are two types of goal of this game. One is to minimize the number of captured rooks, and the other is to maximize it.

In this problem, you are requested to calculate the minimum and maximum values of the number of captured rooks.

Input

The input consists of a single test case in the format below.

$N$ $M$ $x_{1}$ $y_{1}$ $\vdots$ $x_{M}$ $y_{M}$

The first line contains two integers $N$ and $M$ which are the size of the chessboard and the number of rooks, respectively ($1 \le N, M \le 1000$). Each of the following $M$ lines gives the position of each rook. The $i$-th line with $x_{i}$ and $y_{i}$ means that the $i$-th rook is in the $x_{i}$-th column and $y_{i}$-th row ($1 \le x_{i}, y_{i} \le N$). You can assume any two rooks are not in the same place.

Output

Output the minimum and maximum values of the number of captured rooks separated by a single space.

8 3
1 1
1 8
8 8

1 2

8 4
1 1
1 8
8 8
8 1

2 3

5 5
1 1
2 2
3 3
4 4
5 5

0 0

100 1
100 100

0 0

10 12
1 2
1 4
1 6
3 6
5 6
10 7
8 7
6 7
4 7
2 7
7 3
9 5

7 8