F: n 角錐グラフ
問題
$n$ 角錐グラフを以下のように定義する。
- 頂点数は $n + 1$ である。
- 頂点 $0$ と自身を除くすべての頂点との間に、重み付きの無向辺が張られている。
- 頂点 $1, 2, …, n$ はこの順にサイクルとなるように、重み付きの無向辺が張られている。
あなたは $n$ 角錐グラフ上の頂点 $0$ を出発し、異なる $k$ 個の辺を通って頂点 $0$ に戻ってくる必要がある。一度通った辺は,たとえ向きが異なっても二度と通ることはできない。 同じ頂点を何回通っても構わないし、途中で頂点 $0$ を通っても構わない。
これを満たす道順を良いサーキットと呼ぶ。より形式的には、以下のように定義される。
$n$ 角錐グラフの辺からなる集合を $E$ とよび、辺 $e \in E$ の重みを $w(e)$ と書く。 ここで、$n$ 角錐グラフの頂点の列 $(v_1, …, v_{k + 1})$ であり、以下の条件を満たすものを長さ $k$ の良いサーキットとよぶ。
- すべての $1 \leq i \leq k$ に対して $\{v_i, v_{i + 1}\} \in E$
- $v_1 = v_{k + 1} = 0$
- すべての $1 \leq i, j \leq k$ に対して、$i \neq j$ ならば $\{v_i, v_{i + 1}\} \neq \{v_j, v_{j + 1}\}$
また、長さ $k$ の良いサーキットのコストを、通った辺の重みの総和 $\sum_{i = 1}^{k} w(\{v_i, v_{i + 1}\})$ と定義する。
長さ $k$ の良いサーキットすべてについてコストを求め、その総和を $998244353$ で割った余りを出力せよ。長さ $k$ の良いサーキットが存在しない場合は、$0$ を出力せよ。 ただし、二つの長さ $k$ の良いサーキット $(v_1, …, v_{k + 1})$ と $(v'_1, …, v'_{k + 1})$ が異なるとは、$v_i \neq v'_i$ を満たす $i$ ($1 \leq i \leq k+1$) が存在することを言う。
入力形式
入力は $3$ 行からなる。
$1$ 行目には $n$ と $k$ が空白区切りで与えられる。
$2$ 行目と $3$ 行目には、$n$ 角錐グラフの重みを表す長さ $n$ の配列 $A=(a_1, ..., a_n)$ と $B=(b_1, ..., b_n)$ がそれぞれ空白区切りで与えられる。 $a_i$ は、辺 $\{0, i\}$ の重みを表し、$b_i$ は、辺 $\{i, i + 1\}$(ただし、$i = n$ のときは 辺 $\{n, 1\}$)の重みを表す。
$n$ $k$ $a_1$ ... $a_n$ $b_1$ ... $b_n$
制約
- 入力は全て整数で与えられる
- $3 \leq n \leq 10^6$
- $3 \leq k \leq 2n$
- $1 \leq a_i, b_i \leq 10^9$
出力形式
長さ $k$ の良いサーキットすべてに対してコストを求め、その総和を $998244353$ で割った余りを一行に出力せよ。良いサーキットが存在しない場合は $0$ を一行に出力せよ。
入力例1
3 4 1 2 3 4 4 4
出力例1
72
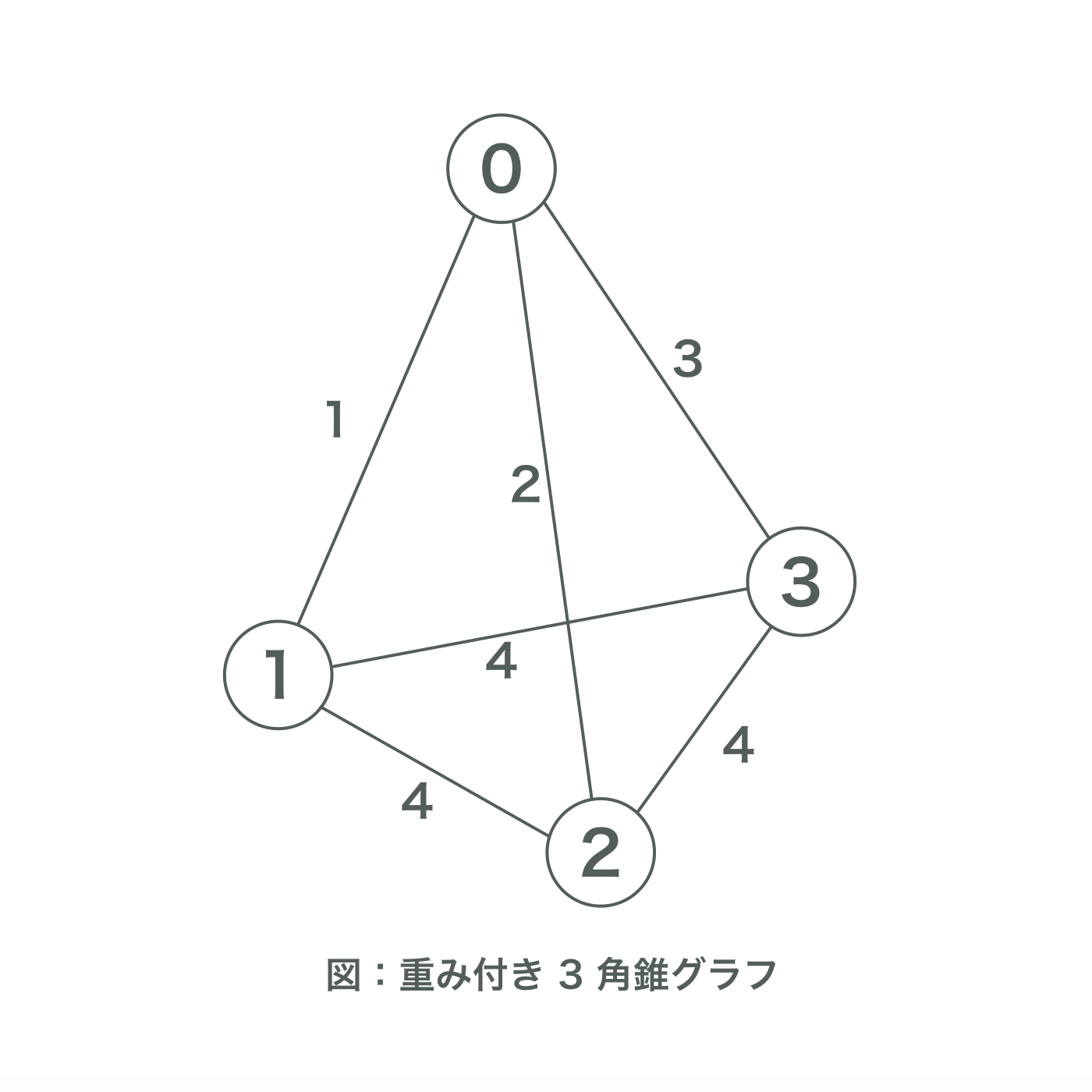
この入力例は上図の $3$ 角錐グラフを表す。
長さ $4$ の良いサーキットとコストは全部で $6$ 個存在する。
- $(0, 1, 2, 3, 0)$
- $(0, 2, 3, 1, 0)$
- $(0, 3, 1, 2, 0)$
- $(0, 3, 2, 1, 0)$
- $(0, 1, 3, 2, 0)$
- $(0, 2, 1, 3, 0)$
コストはそれぞれ、$12$、$11$、$13$、$12$、$11$、$13$ である。 よって、これらを足し合わせた $72$ を出力する。
入力例2
4 6 1 1 3 4 4 3 1 2
出力例2
224
長さ $6$ の良いサーキットの一例として、$(0, 1, 2, 0, 3, 4, 0)$ が挙げられる。