アローダイス

アローダイス (arrow dice) とは，立方体の各面の中央部にその面を構成する 4 辺のいずれかの中心を向いた矢印が 1 つずつ書かれたものである．図 F-1 にその一例を示す．

図 F-1 アローダイスの一例

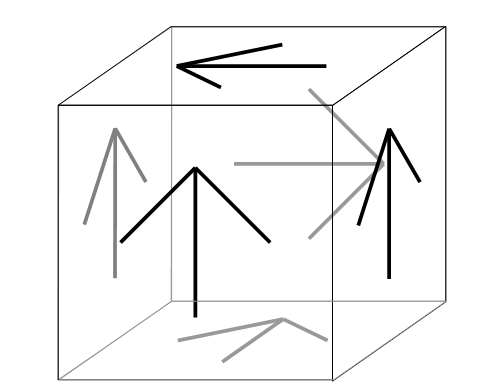
ここで，2 つのアローダイスの相違度を「それぞれを任意に回転させたあとで立方体として完全に重なり合うように重ね合わせたときに，対応する面について向きの異なる矢印の個数の最小値」と定義する．

n 個のアローダイスが与えられるので，すべてのペアに対してその相違度を求めてほしい．

Input

入力は最大 50 データセットからなり，各データセットは次の形式で表される．

n
x_1,1x_1,2...x_1,5
x_2,1x_2,2...x_2,5
...
x_5n,1x_5n,2...x_5n,5

各データセットの 1 行目には与えられるアローダイスの個数 n (2 ≤ n ≤ 200)，続く 5n 行には n 個のアローダイスの情報が 5 行ずつ与えられる．5i-4 行目から 5i 行目までの入力が i 個目のアローダイスの情報である．

各アローダイスは 5 × 5 のグリッドで表現される． グリッド上で '^', 'v', '<', '>' はそれぞれ上下左右を向いた矢印が書かれたマスを表し，'.' は余白を表す． グリッドから余白を取り除いて得られる図形に対して，隣接するマスの間を山折りにして得られる立体がこのグリッドが表現するアローダイスである．入力として与えられるどの図形に関しても，正しく組み立てることでアローダイスが 1 つ出来上がることが保証されている． 例えば，サンプルの最初のケースの 1 つ目の入力が表す図形は図 F-2 の通りであり，図 F-1はこれを組み立てて得られるアローダイスを表している．

図 F-2

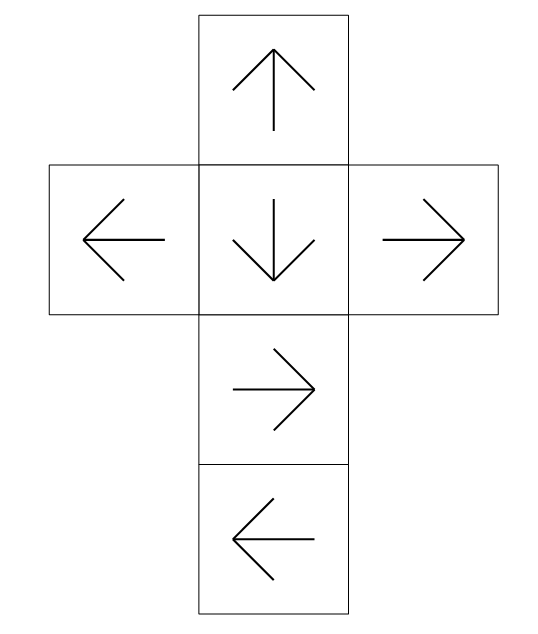
入力の終わりは 1 つのゼロからなる行で表される．

Output

各データセットに対して，i 行目の j 文字目に i 個目のアローダイスと j 個目のアローダイスの相違度を出力せよ．つまり，長さ n の数字列を n 行出力することになる．なお，2 つのアローダイスの相違度は 1 桁の整数となることが証明できる．

Sample Input

3
..^..
.<v>.
..>..
..<..
.....
..^..
.<^>.
..>..
..<..
.....
..>..
..^v.
.^>..
.v...
.....
8
..<^.
...^<
...<.
...<.
.....
.<...
<>...
.^<..
.v...
.....
.....
.....
.>...
^>><.
<....
.....
...<.
..v^.
..>..
.<v..
.....
...<.
..^v.
...<>
...>.
.....
...^.
..>v.
.v^..
.<...
.....
..<..
.vv..
^v...
.^...
.....
....>
.v^vv
...<.
.....
0

Output for the Sample Input

010
101
010
02222232
20432043
24013422
23103331
22330223
20432043
34232402
23213320

---