8 Queens Problem

The goal of 8 Queens Problem is to put eight queens on a chess-board such that none of them threatens any of others. A queen threatens the squares in the same row, in the same column, or on the same diagonals as shown in the following figure.

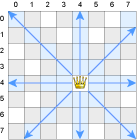
For a given chess board where $k$ queens are already placed, find the solution of the 8 queens problem.

Input

In the first line, an integer $k$ is given. In the following $k$ lines, each square where a queen is already placed is given by two integers $r$ and $c$. $r$ and $c$ respectively denotes the row number and the column number. The row/column numbers start with 0.

Output

Print a $8 \times 8$ chess board by strings where a square with a queen is represented by 'Q' and an empty square is represented by '.'.

Constraints

• There is exactly one solution

Sample Input 1

2
2 2
5 3

Sample Output 1

......Q.
Q.......
..Q.....
.......Q
.....Q..
...Q....
.Q......
....Q...

---