Rooted Trees
A graph G = (V, E) is a data structure where V is a finite set of vertices and E is a binary relation on V represented by a set of edges. Fig. 1 illustrates an example of a graph (or graphs).
Fig. 1
A free tree is a connnected, acyclic, undirected graph. A rooted tree is a free tree in which one of the vertices is distinguished from the others. A vertex of a rooted tree is called "node."
Your task is to write a program which reports the following information for each node u of a given rooted tree T:
- node ID of u
- parent of u
- depth of u
- node type (root, internal node or leaf)
- a list of chidlren of u
If the last edge on the path from the root r of a tree T to a node x is (p, x), then p is the parent of x, and x is a child of p. The root is the only node in T with no parent.
A node with no children is an external node or leaf. A nonleaf node is an internal node
The number of children of a node x in a rooted tree T is called the degree of x.
The length of the path from the root r to a node x is the depth of x in T.
Here, the given tree consists of n nodes and evey node has a unique ID from 0 to n-1.
Fig. 2 shows an example of rooted trees where ID of each node is indicated by a number in a circle (node). The example corresponds to the first sample input.
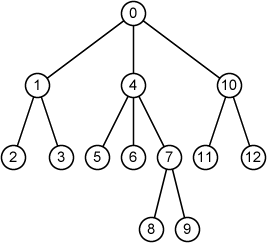
Fig. 2
Input
The first line of the input includes an integer n, the number of nodes of the tree.
In the next n lines, the information of each node u is given in the following format:
id k c1 c2 ... ck
where id is the node ID of u, k is the degree of u, c1 ... ck are node IDs of 1st, ... kth child of u. If the node does not have a child, the k is 0.
Output
Print the information of each node in the following format ordered by IDs:
node id: parent = p, depth = d, type, [c1...ck]
p is ID of its parent. If the node does not have a parent, print
d is depth of the node.
type is a type of nodes represented by a string (root, internal node or leaf). If the root can be considered as a leaf or an internal node, print root.
c1...ck is the list of children as a ordered tree.
Please follow the format presented in a sample output below.
Constraints
- 1 ≤ n ≤ 100000
Sample Input 1
13 0 3 1 4 10 1 2 2 3 2 0 3 0 4 3 5 6 7 5 0 6 0 7 2 8 9 8 0 9 0 10 2 11 12 11 0 12 0
Sample Output 1
node 0: parent = -1, depth = 0, root, [1, 4, 10] node 1: parent = 0, depth = 1, internal node, [2, 3] node 2: parent = 1, depth = 2, leaf, [] node 3: parent = 1, depth = 2, leaf, [] node 4: parent = 0, depth = 1, internal node, [5, 6, 7] node 5: parent = 4, depth = 2, leaf, [] node 6: parent = 4, depth = 2, leaf, [] node 7: parent = 4, depth = 2, internal node, [8, 9] node 8: parent = 7, depth = 3, leaf, [] node 9: parent = 7, depth = 3, leaf, [] node 10: parent = 0, depth = 1, internal node, [11, 12] node 11: parent = 10, depth = 2, leaf, [] node 12: parent = 10, depth = 2, leaf, []
Sample Input 2
4 1 3 3 2 0 0 0 3 0 2 0
Sample Output 2
node 0: parent = 1, depth = 1, leaf, [] node 1: parent = -1, depth = 0, root, [3, 2, 0] node 2: parent = 1, depth = 1, leaf, [] node 3: parent = 1, depth = 1, leaf, []
Note
You can use a left-child, right-sibling representation to implement a tree which has the following data:
- the parent of u
- the leftmost child of u
- the immediate right sibling of u
Reference
Introduction to Algorithms, Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. The MIT Press.