木の巡回

以下に示すアルゴリズムで、与えられた２分木のすべての節点を体系的に訪問するプログラムを作成してください。

1. 根節点、左部分木、右部分木の順で節点の番号を出力する。これを木の先行順巡回 (preorder tree walk) と呼びます。
2. 左部分木、根節点、右部分木の順で節点の番号を出力する。これを木の中間順巡回 (inorder tree walk) と呼びます。
3. 左部分木、右部分木、根節点の順で節点の番号を出力する。これを木の後行順巡回 (postorder tree walk) と呼びます。

与えられる２分木は $n$ 個の節点を持ち、それぞれ $0$ から $n-1$ の番号が割り当てられているものとします。

入力

入力の最初の行に、節点の個数 $n$ が与えられます。続く $n$ 行目に、各節点の情報が以下の形式で１行に与えられます。

$id$ $left$ $right$

$id$ は節点の番号、$left$ は左の子の番号、$right$ は右の子の番号を表します。子を持たない場合は $left$ ($right$) は -1 で与えられます。

出力

１行目に"Preorder"と出力し、２行目に先行順巡回を行った節点番号を順番に出力してください。

３行目に"Inorder"と出力し、４行目に中間順巡回を行った節点番号を順番に出力してください。

５行目に"Postorder"と出力し、６行目に後行順巡回を行った節点番号を順番に出力してください。

節点番号の前に１つの空白文字を出力してください。

制約

• $1 \leq n \leq 25$

入力例 1

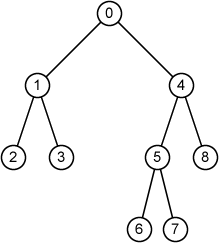
9
0 1 4
1 2 3
2 -1 -1
3 -1 -1
4 5 8
5 6 7
6 -1 -1
7 -1 -1
8 -1 -1

出力例 1

Preorder
 0 1 2 3 4 5 6 7 8
Inorder
 2 1 3 0 6 5 7 4 8
Postorder
 2 3 1 6 7 5 8 4 0

参考文献

Introduction to Algorithms, Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. The MIT Press.

---