Note
完全二分木
すべての葉が同じ深さを持ち、すべての内部節点の次数が 2 であるような二分木を完全二分木と呼びます。また、二分木の最下位レベル以外のすべてのレベルは完全に埋まっており、最下位レベルは最後の節点まで左から順に埋まっているような木も(おおよそ)完全二分木と呼びます。
二分ヒープは、次の図のように、木の各節点に割り当てられたキーが1つの配列の各要素に対応した完全二分木で表されたデータ構造です。
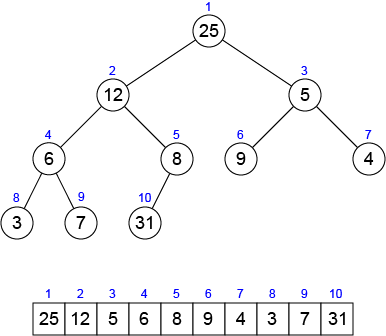
二分ヒープを表す配列を $A$、二分ヒープのサイズ(要素数)を $H$ とすれば、$A[1...H]$ に二分ヒープの要素が格納されます。木の根の添え字は $1$ であり、節点の添え字 $i$ が与えられたとき、その親 $parent(i)$、左の子 $left(i)$、右の子 $right(i)$ はそれぞれ $\lfloor i / 2 \rfloor$、$2 \times i$、$2 \times i + 1$ で簡単に算出することができます。
完全二分木で表された二分ヒープを読み込み、以下の形式で二分ヒープの各節点の情報を出力するプログラムを作成してください。
node $id$: key = $k$, parent key = $pk$, left key = $lk$, right key = $rk$,
ここで、$id$ は節点の番号(インデックス)、$k$ は節点の値、$pk$ は親の値、$lk$ は左の子の値、$rk$ は右の子の値を示します。これらの情報をこの順番で出力してください。ただし、該当する節点が存在しない場合は、出力を行わないものとします。
入力
入力の最初の行に、二分ヒープのサイズ $H$ が与えられます。続いて、ヒープの節点の値(キー)を表す $H$ 個の整数がそれらの節点の番号順に空白区切りで与えられます。
出力
上記形式で二分ヒープの節点の情報をインデックスが 1 から $H$ に向かって出力してください。各行の最後が空白となることに注意してください。
制約
- $H \leq 250$
- $-2,000,000,000 \leq 節点のキー \leq 2,000,000,000$
入力例 1
5 7 8 1 2 3
出力例 1
node 1: key = 7, left key = 8, right key = 1, node 2: key = 8, parent key = 7, left key = 2, right key = 3, node 3: key = 1, parent key = 7, node 4: key = 2, parent key = 8, node 5: key = 3, parent key = 8,
参考文献
Introduction to Algorithms, Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. The MIT Press.