的当ての判定
図のような頂点$A(0,d)$、$B(d,0)$、$C(0,-d)$、$D(-d,0)$で囲まれた正方形の的があります。この的に向かって矢を投げ、正方形の内部か辺の上に刺されば矢が的に当たったと判定されて賞品がもらえます。
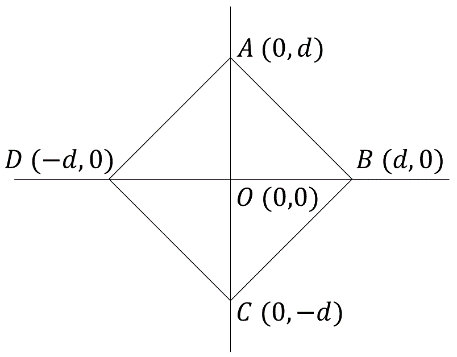
矢が点$P(x,y)$に刺さったとき、矢が的に当たったかどうかは、以下のように判定できます。原点Oからx軸に沿って座標$(x,0)$まで進んだ後、y軸と平行に点$P$まで進む道のりを考えます。この道のりに沿って長さを測り、それが$d$以下かどうかを調べることで判定できます。
たとえば、$d=6$で、矢が点$(2,3)$に刺さったとします。このとき、原点Oから点$(2,0)$までx軸に沿って2進み、そこから点$(2,3)$までy軸に平行に3進む道のりを考えます。この道のりの長さは$2+3=5$です。$5 \leq d = 6$なので、矢は的に当たったことがわかります。
$d$の値と矢が刺さった点$P$の座標が与えられたとき、矢が的に当たったかどうかを判定するプログラムを作成せよ。
入力
入力は以下の形式で与えられる。
$d$ $x$ $y$
1行に正方形の大きさを示す数$d$ ($1 \leq d \leq 100,000$)、点$P$のx座標($-100,000 \leq x \leq 100,000$)、点$P$のy座標($-100,000 \leq y \leq 100,000$)が与えられる。
出力
矢が的に当たっていれば「Yes」、そうでなければ「No」を1行に出力する。
入出力例
入力例1
5 3 2
出力例1
Yes
入力例2
5 0 -8
出力例2
No
参考
この問題で測った原点から点$P$までの道のりの長さを、原点から点$P$までのマンハッタン距離と呼びます。点$\alpha (x_1,y_1)$から点$\beta (x_2,y_2)$までのマンハッタン距離は、$d_1 (\alpha,\beta)=|x_2-x_1|+|y_2-y_1|$として計算します。記号$|x|$は$x$の絶対値を意味します。