基本的な考え方は前問 Linear Search と同じで、探索によって数列 $S$ の中に、$T$ の各要素が含まれているかを調べます。ただし、$O(n)$ の線形探索では制限時間内に処理を終えることはできません。今回は「$S$ の要素が昇順に整列されている」という制約を有効利用し、二分探索を適用することができます。
コンピュータで扱うデータは、多くの場合ある項目によって整列され管理されています。なぜなら、整列されたデータは検索しやすいからです。二分探索(二分検索)は、データの大小関係を利用した高速な探索アルゴリズムです。
データがキーの昇順に配列に格納されているとすると、二分探索のアルゴリズムは次のようになります。
- 配列全体を探索の範囲とします。
- 探索の範囲内の中央の要素を調べます。
- 目的のキーと中央の要素のキーが一致すれば探索を終了します。
- 目的のキーが中央の要素のキーよりも小さければ前半部分を、大きければ後半部分を探索の範囲として 2. へ戻ります。
要素数が $n$ の配列 $A$ から、$key$ を探す二分探索のアルゴリズムは次のようになります。
binarySearch()
left = 0
right = n
while left < right
mid = (left + right) / 2
if A[mid] == key
return mid
else if key < A[mid]
right = mid
else
left = mid + 1
return NOT_FOUND
二分探索の実装では、次のように、探索範囲を表すための変数left、right、中央の位置を指すmid を用います。

left は探索範囲の先頭の要素を指し、right は末尾の次の要素を指します。mid は left と right を足して2で割った値(小数点以下は切捨て)になります。
具体的な例を見てみましょう。次の図は、昇順に整列された 14 個の要素を含む配列から、二分探索により36 を探す様子です。
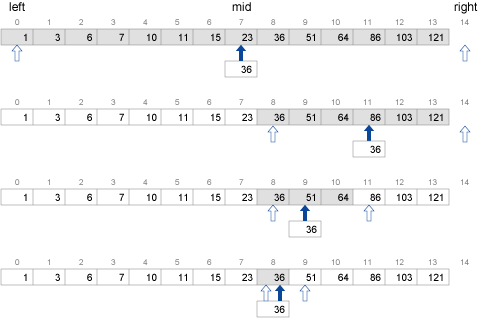
二分探索は最初データの全体を探索の範囲とするので、left を 0 に、right を要素数 N に初期化します。
while ループで、現時点の探索範囲の真ん中の位置 mid を (left + right)/2 で求め、mid が指す要素 A[mid] と key を比較していきます。一致している場合は mid を返します。key が A[mid] よりも小さい場合、目的の値は mid よりも前にあるので、right を mid とすることで探索範囲を前半部分にします。逆の場合は left を mid + 1 とすることで探索範囲を後半部分にします。上の例では、最初のステップで key(=36) は中央の値 A[mid] よりも大きいので、left を 8 に設定しています(8より前を探索するのは無駄であることが分かります)。
while ループの繰り返し条件 left < right は、探索範囲がまだ存在することを示し、もし探索範囲がなくなってしまったら、key が発見できなかったとして NOT_FOUND を返します。
次の表は、要素数が $n$ の配列を対象とした線形探索と二分探索のそれぞれの最悪の比較演算の回数です。
| 要素数 | 線形探索 | 二分探索 |
|---|---|---|
| 100 | 100 回 | 7 回 |
| 10,000 | 10,000 回 | 14 回 |
| 1,000,000 | 1,000,000 回 | 20 回 |
最悪の比較回数は、線形探索の場合 $n$ 回、二分探索の場合はおおよそ $log_2 \;n$ 回になります。二分探索の計算効率が $O(log\;n)$ となるのは、一回の比較演算を行うごとに探索の範囲が半分になっていくという性質から容易に導き出すことができます。
この問題(ALDS1_4_C: Binary Search)は、$T$ の各要素について二分探索を行って $O(q\;log\;n)$ のアルゴリズムで解くことができます。
この問題では、入力の配列が整列された状態で与えられましたが、そうでない場合でも、前処理としてあらかじめ整列を行えば二分探索を適用することができます。このように、「整列すれば二分探索が使える」という考え方は様々な問題に応用することができます。ただし、データの大きさを考えると、ほとんどの場合、高等的なソートアルゴリズムが必要になります。
Reference

|
プログラミングコンテスト攻略のためのアルゴリズムとデータ構造 (マイナビ)AIZU ONLINE JUDGE のコース問題を題材にした解説書です。初級者が体系的にアルゴリズムとデータ構造の基礎を学ぶことができる入門書となっています。 |