ALDS1_5_A:

この問題は、$n$ の値が小さいので、数列の要素を選ぶ組み合わせを列挙するアルゴリズムが適用できます。各要素について選択するかしないかの2択となるので、$2^n$ 通りの組み合わせがあります。これらは次の再帰によるアルゴリズムで生成することができます。

1  makeCombination()
2    for i = 0 to n-1
3      S[i] = 0 // i を選択しない
4    rec(0)
5
6  rec(i)
7    if i == n
8      print S
9      return
10
11   rec(i + 1)
12   S[i] = 1 // i を選択する
13   rec(i + 1)
14   S[i] = 0 // i を選択しない

S を S[i] が 1 のとき i 番目の整数を選択する、0 のとき選択しない、という配列とします。最初の要素から選択するかしないかを再帰関数によって分岐させ、 i が $n$ に達したときの S が１つの組み合わせを保持しています。0 から $2^n$ − 1までのビット列が生成されることになります。

この再帰関数により、i 番目の要素を選ぶか選ばないかの全ての組み合わせを調べることができます。例えば、$n$ が 3 のとき rec(0) は S に記録されるビット列として、{0, 0, 0}, {0, 0, 1}, {0, 1, 0}, {0, 1, 1},{1, 0, 0}, {1, 0, 1}, {1, 1, 0}, {1, 1, 1} を順番に生成します。

ここでは、この考え方を応用し、次のような１つの関数を定義して問題を解くことにします。solve(i, m)を「i 番目以降の要素を使って m を作れる場合 true を返す」という関数とすると、solve(i, m) はより小さい部分問題である solve(i+1, m) と solve(i+1, m - A[i]) に分割することができます。ここで、A[i] を引いていることが、「i 番目の要素を使う」に対応しています。これらを再帰的に調べることで元の問題である solve(0, m) を判定することができます。

1 solve(i, m)
2   if m == 0
3     return true
4   if i >= n
5     return false
6   res = solve(i + 1, m) || solve(i + 1, m - A[i])
7   return res

solve(i, m) において、与えられた整数を作ることができたとき、m が 0 となります。また m が 0 より大きくかつ i が $n$ 以上になったときに与えられた整数は作れなかったことになります。部分問題である solve(i+1, m) か solve(i+1, m - A[i]) のいずれかが trueのとき、元の問題 solve(i, m) が true になります。

例えば、次の例は数列 A = {1, 5, 7} に対して、8 が作れるかどうかを判定している様子です。

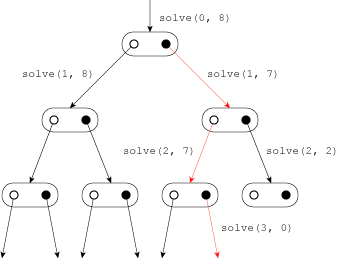
この例では、「1 を選ぶ」$\rightarrow$ 「5 を選ばない」$\rightarrow$「7 を選ぶ」の組み合わせで8 を作ることができます。関数の中で i 番目の要素を選ぶか選ばないかについてさらに２つの関数を呼び出します。

再帰関数の中で２つの再帰関数を呼び出すことを繰り返せば、$O(2^n)$ のアルゴリズムとなり、全ての組み合わせを調べる方法は大きな $n$ に対しては適用することができません。このアルゴリズムでは (i, m) の組について solve(i, m) が複数回計算されてしまう無駄があります。これは動的計画法と呼ばれるテクニックで改善することができます。

Reference

プログラミングコンテスト攻略のためのアルゴリズムとデータ構造 (マイナビ) AIZU ONLINE JUDGE のコース問題を題材にした解説書です。初級者が体系的にアルゴリズムとデータ構造の基礎を学ぶことができる入門書となっています。