ALDS1_5_C:

コッホ曲線の頂点の座標を順番に出力する再帰関数は次のようになります。

kock(n, p1, p2)
    if n == 0
        return

    // p1, p2 から s, t, u を計算

    kock(n-1, p1, s)
    print s
    kock(n-1, s, u)
    print u
    kock(n-1, u, t)
    print t
    kock(n-1, t, p2)

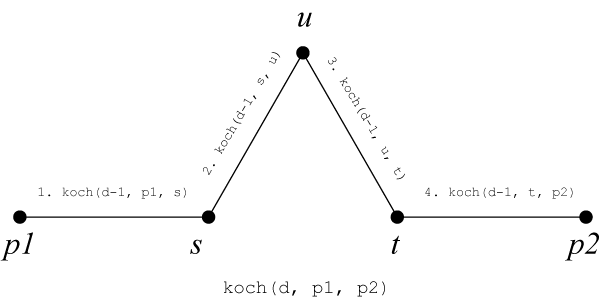
関数 koch は、再帰の深さを表す $d$ と、線分の端点 $p1$、$p2$ を引数とします。この再帰関数では図のようにまず、線分 $p1p2$ からそれを三等分するような点 $s$、$t$ を求め、線分 $su$、$ut$、$ts$ が正三角形を成すような点 $u$ を求めます。続いて、以下の処理を順番に行い線分を描画します。

1. 線分 $p1s$ に対して koch を再帰的に呼び出し、$s$ の座標を出力。
2. 線分 $su$ に対して koch を再帰的に呼び出し、$u$ の座標を出力。
3. 線分 $ut$ に対して koch を再帰的に呼び出し、$t$ の座標を出力。
4. 線分 $tp2$ に対して koch を再帰的に呼び出す。

$u$ の座標はベクトル演算で求めることができます。まず、$s$ と $t$ の座標は以下の式で求めることができます。

$s.x = \frac{(2 \times p1.x + 1 \times p2.x)}{3}$
$s.y = \frac{(2 \times p1.y + 1 \times p2.y)}{3}$
$t.x = \frac{(1 \times p1.x + 2 \times p2.x)}{3}$
$t.y = \frac{(1 \times p1.y + 2 \times p2.y)}{3}$

点 $u$ は、点 $t$ を点 $s$ を起点として反時計回りに 60 度回転した位置にあります。ここで、原点中心の回転速度に使われる回転行列を用いると、点 $u$ は次の式で求めることができます。

$u.x = (t.x − s.x) \times cos 60^\circ − (t.y − s.y) \times sin60^\circ + s.x$
$u.y = (t.x − s.x) \times sin 60^\circ + (t.y − s.y) \times cos60^\circ + s.y$

初期状態の端点 $p1$, $p2$ に対して koch を呼び出せば、$p1$ から $p2$ にいたる全ての頂点を順番に出力することができます。

Reference

プログラミングコンテスト攻略のためのアルゴリズムとデータ構造 (マイナビ) AIZU ONLINE JUDGE のコース問題を題材にした解説書です。初級者が体系的にアルゴリズムとデータ構造の基礎を学ぶことができる入門書となっています。